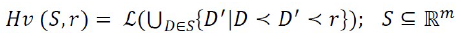1. Introduction
Optimization is the process of finding the best solution within a set of possible solutions. In practical engineering problems, most applications are non-linear, have complicated or nonexistent analytical solutions, and must serve multiple objectives or functions that may conflict [
1]. Multi-objective optimization is a technique used to optimize multiple conflicting objectives simultaneously while considering constraints. In this approach, a set of objective functions is defined, and the goal is to find solutions that represent a trade-off among these objectives, as improving one objective may lead to degradation in another. The aim is to identify a set of solutions known as the Pareto front, where no other solution can improve one objective without worsening at least one other [
2]. Multi-objective optimization is essential for addressing complex pharmaceutical problems where decision-making involves balancing multiple criteria or goals [
3,
4].
Multi-objective optimization is a systematic approach that involves formulating a problem, selecting an appropriate optimization algorithm, and executing it to identify the Pareto-optimal front. This front is a set of solutions where no single solution can improve performance in one objective without sacrificing performance in another. After running the algorithm, the results are reviewed to analyze the inherent trade-offs between the objectives and decision variables. Results are typically presented across objective space, decision variable space, and objective versus decision variable space, providing insights into the relationships and dependencies between these parameters. Furthermore, Pareto optimal solutions constitute a collection of outcomes in a multi-objective optimization problem wherein no solution can be enhanced in one objective without compromising another. This means that every solution in this set is non-dominated, signifying that no other solution surpasses it in all objectives simultaneously. The aggregation of these solutions defines the Pareto front, representing the optimal trade-offs achievable among the competing objectives [
5]. Finally, from the set of non-dominated Pareto-optimal solutions, a single optimal solution is chosen based on the relative importance of the objectives and the preferences of decision-makers or stakeholders [
6].
This study focuses on biodegradable polymers, particularly synthetic ones like polylactic acid (PLA), which have garnered interest in drug delivery systems. The PLA and polyvinylpyrrolidone K30 (PVP K30) are commonly employed in pharmaceutical microencapsulation for controlled drug release. This is owing to their non-toxic and well-tolerated properties. This study aims to optimize a biodegradable micro-polymeric carrier system using MOO algorithms. The system is based on PVP K30 and PLA, with model representations derived from a previous experimental study [
7]. The optimization process uses multi-objective optimization algorithms to improve bioavailability and extend the release of candesartan cilexetil antihypertensive drug. Therefore, the objectives are to maximize encapsulation efficiency while simultaneously maximizing drug release.
2. Methodology
This study was based on Response Surface Methodology (RSM) models (Equations (1) and (2)) to optimize the formulation of candesartan cilexetil microencapsulation using biodegradable polymers [
7]. The mixed factorial design was used to develop mathematical models that correlate encapsulation efficiency and cumulative drug release at 12 h with the levels of various formulation factors. The study used two primary biodegradable polymers: polylactic acid (PLA) and polyvinylpyrrolidone (PVP K30). PLA is a biodegradable polyester with excellent chemical and physical properties, suitable for drug delivery systems. The concentrations of poly(lactic acid) (PLA) were evaluated within the range of 100 mg to 300 mg. The addition of PLA concentrations enhanced encapsulation efficiency by facilitating the formation of a more compact polymer network. However, an excessive amount of PLA may hinder drug release, as the dense matrix restricts the diffusion of the drug into the surrounding medium.
PVP K30, a hydrophilic polymer, plays a significant role in modulating the drug release profile. As a pore-forming agent, increasing concentrations of PVP K30 (ranging from 0 mg to 100 mg) facilitate the penetration of the dissolution medium into the microcapsule, resulting in an accelerated drug release. Consequently, PVP K30 is recognized as a valuable component for enhancing the bioavailability of poorly soluble drugs. The interaction between PLA and PVP K30 is critical, as achieving an optimal balance between these components ensures effective drug encapsulation while preserving desirable release rates. Furthermore, the volume of PVA (V-PVA) solution (1%
w/
v), which varies between 50 mL and 75 mL, significantly impacts the stability and size of the microcapsules. The encapsulation duration, ranging from 0 to 12 h, plays a crucial role in the degree of polymer solidification. This, in turn, impacts both the structural integrity of the microcapsules and the efficiency of the encapsulation process.
The study found that the ratio of polymer to active ingredient influences the encapsulation efficiency of candesartan cilexetil. Higher polymer ratios increase efficiency but may hinder drug release. Formulations with a PLA: drug ratio of 6:1 showed maximum efficiencies of 68%–71%. However, formulations with higher polymer content may reduce bioavailability. The study suggested optimizing formulations balances encapsulation efficiency and drug release to improve overall bioavailability [
7].
The procedure of performing MOO can be summarized in the following five steps:
1. The use of the RSM models as problem definition for each objective (Equations (1) and (2)):
where
Y1 represents the Encapsulation efficiency, and
Y2 represents the percentage of drug release at 12 h.
PLA,
VPVA, and
PVP represent polylactic acid amount, volume of 1% polyvinyl alcohol and polyvinylpyrrolidone K30 amount, respectively.
2. The utilization of five multi-objective algorithms, including the Reference point based Non-dominated Sorting Genetic Algorithm III (NSGA-III) [
8], a Multi-objective Evolutionary Algorithm Based on Decomposition (MOEAD) [
9], a Reference Vector guided Evolutionary Algorithm for many-objective optimization (RVEA) [
10], a Two-Archive Evolutionary Algorithm for Constrained Multi-objective Optimization (C-TAEA) [
11], and an Adaptive Geometry Estimation based Many-Objective Evolutionary Algorithm (AGE-MOEA) [
12].
The NSGA-III is predicated on a reference point methodology that facilitates concurrently managing multiple reference points, thereby enabling users to concentrate on particular areas of the Pareto-optimal front. Its advantages are evident in its capacity to adeptly navigate conflicting objectives through the application of guided reference directions, which aids in the identification of diverse trade-off solutions. This approach significantly enhances decision-making by offering a well-distributed array of near-Pareto-optimal solutions, even within high-dimensional objective spaces. This algorithm upholds a systematic approach to the distribution of solutions, thereby ensuring a well-converged and diverse array of solutions along the Pareto-optimal front. Furthermore, the normalization process employed by NSGA-III, along with its methodical assignment of reference directions, significantly enhances its efficiency and effectiveness in navigating complex objective spaces [
8].
The MOEA/D method decomposes a multi-objective optimization problem into multiple scalar optimization subproblems, which are simultaneously optimized using a population of solutions. The algorithm’s strengths are evident in its ability to effectively manage conflicting objectives by leveraging neighborhood relationships among the subproblems. This approach enables a more thorough exploration of the solution space and encourages a more uniform distribution of optimal solutions. Furthermore, MOEA/D is capable of integrating various decomposition strategies, thereby increasing its adaptability to a diverse range of multi-objective problems. The Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) presents several advantages in comparison to alternative algorithms. Notably, it exhibits reduced computational complexity at each generation, facilitating expedited processing. Additionally, MOEA/D has been shown to achieve higher solution quality in multi-objective knapsack problems and continuous test instances, particularly when employing advanced decomposition techniques. Moreover, MOEA/D adeptly addresses challenges associated with fitness assignment and diversity maintenance, thereby enhancing its efficiency in optimizing scalar problems relative to non-decomposition approaches [
9].
The Reference Vector Guided Evolutionary Algorithm (RVEA) is specifically designed to address many-objective optimization problems. RVEA integrates the principles of dominance and decomposition, effectively leveraging the advantages of both methodologies to manage multiple conflicting objectives. It introduces a scalarization technique known as Angle Penalized Distance, which dynamically balances convergence and diversity within high-dimensional objective spaces, thereby addressing the inherent challenges associated with many-objective problems. The algorithm employs reference vectors to direct the search process toward preferred regions of the Pareto front, facilitating a more focused exploration of the solution space in accordance with user preferences. Furthermore, RVEA incorporates mechanisms to preserve population diversity, a critical factor in high-dimensional contexts where solutions may become sparse. This feature enhances the algorithm’s ability to approximate the Pareto front more effectively. The performance of RVEA has been empirically validated against several state-of-the-art multi-objective evolutionary algorithms across a variety of benchmark problems, demonstrating its robust capabilities [
10].
The C-TAEA algorithm, on the other hand, uses two archives—one for feasible solutions (CA) and another for infeasible solutions (DA)—enabling it to maintain diversity while effectively exploring both feasible and infeasible regions of the solution space. By concurrently managing both archives, C-TAEA strikes a balance between the search for feasible solutions and the preservation of diversity within the population, which is essential when addressing conflicting objectives. The algorithm employs various constraint-handling techniques, such as prioritizing feasible solutions and applying a constrained dominance relation that combines both objective and constraint rankings for solution evaluation. Additionally, it employs a modified version of nondominated sorting that considers both objective values and constraints in ranking solutions, thereby enhancing the search for optimal outcomes. The efficacy of C-TAEA has been empirically validated against leading constrained evolutionary multi-objective optimizers and a range of engineering and real-world problems, demonstrating its competitiveness across various benchmark scenarios [
11].
The AGE-MOEA is based on evolutionary algorithms specifically designed to tackle multi-objective and many-objective optimization problems. This algorithm approximates the geometry of the generated Pareto front through a computationally efficient process, which is characterized by a complexity of O(M × N), where M signifies the number of objectives and N represents the population size. This efficiency level allows the algorithm to adjust its strategies in alignment with the specific geometric characteristics of the problem being addressed.
AGE-MOEA modifies diversity and proximity metrics in accordance with the estimated geometry of the problem space. This adaptation implies that the selection of solutions for subsequent generations is informed by their contributions to sustaining a well-diversified set of solutions while also ensuring a close approximation to the Pareto front, specifically tailored to the unique characteristics of the problem at hand. By emphasizing both diversity—ensuring a broad distribution of solutions—and proximity—aiming to position solutions near the Pareto optimal front—the algorithm adeptly navigates the trade-offs associated with conflicting objectives. This dual emphasis facilitates the generation of a more comprehensive array of solutions that more accurately reflect the trade-offs between these conflicting objectives. Empirical evaluations have demonstrated that AGE-MOEA significantly surpasses several established multi-objective evolutionary algorithms across a variety of benchmark test problems characterized by differing geometries and numbers of objectives. The findings indicate that AGE-MOEA achieves lower Inverted Generational Distance (IGD) values, which serve as a metric for assessing the quality of the non-dominated front produced [
12].
3. Maximize the entrapment efficiency and drug release objectives and generate comparable Pareto fronts, with a termination criterion set at a maximum of 100 generations.
4. Evaluate the Pareto-optimal set using different performance indicators (Equations (3)–(8)) [
4]:
- The hypervolume metric, denoted as $$Hv\ (S,r)$$, quantifies the size of the space covered by the Pareto-optimal set S in relation to a reference point $$r\in\mathbb{R}^m$$.
where $$\mathcal{L}(·)$$ is the Lebesgue measure,
D and $$D^\prime$$ refer to dominated and non-dominated solutions, respectively, and $$r\in\mathbb{R}^m$$ is a reference point.
- The generational distance (GD) metric measures the convergence of the Pareto-optimal set to the true Pareto front:
where
n represents the number of solutions on the true Pareto front, and $$d_i$$ represents the Euclidean distance of each optimal solution to its nearest solution on the true Pareto-optimal front.
- The inverted generational distance (IGD) metric complements GD by measuring how well the true Pareto front is represented by the generated Pareto set:
where the $${d_i}^\ast$$ represents the Euclidean distance of each solution on the true Pareto-optimal front to its nearest optimal solution, which is the inverse regarding $$d_i$$.
- The spacing metric (SP) assesses the uniformity of the distribution of solutions in the Pareto set:
where
N is the number of solutions in the Pareto set, $$d_n$$ is the Euclidean distance of each solution
n from the mean of the solutions, and $$\overline{d}$$ is the mean of the distances.
- The maximum spread metric (MaxSP) evaluates the extent of the objective space covered by the Pareto set:
where
o denotes the number of objectives, $$a_i$$ and $$b_i$$ are the maximum and minimum values of the
ith objective over all solutions, respectively.
- The spread metric (SM) evaluates both the extent of coverage and the uniformity of the Pareto front:
where
M signifies the number of extreme points, {$$e_1,\ e_2,\ \ldots,\ e_m$$} represent the extreme solutions for
m number objectives, $$d\left(e_m,\ S\right)$$ denotes the Euclidean distance between the extreme solutions and the true Pareto-optimal front, and $$\overline{d}$$ is the average of all $$d_i$$.
5. The selection of a single optimal formulation based on the WSM (Equation (9)):
where $${Score}_{WSM}$$ is the scores for a given Pareto-optimal solution, $$a_i$$ is the value of the
ith objective for an Pareto-optimal solution, $$w_i$$ is the weight assigned to the
ith objective,
n is the total number of objectives.
This method allows for prioritizing certain objectives based on their relative importance, facilitating the selection of a solution that aligns with specific performance criteria [
13].
3. Results and Discussion
3.1. The Conflicting Relationship between Objectives and Pareto Fronts
In a,b, the 3D plots illustrate the relationship between the three variables (PLA, V-PVA, and PVP) and the two objectives (encapsulation efficiency and drug release). Notably, it is observed that the objectives demonstrate opposite trends in terms of their maxima and minima. For instance, while maximizing the encapsulation efficiency, this may entail minimizing the drug release rate. This indicates a trade-off between the two objectives. Encapsulation efficiency and drug release are frequently inversely correlated, a relationship that can be attributed to the characteristics of the encapsulating polymer matrix. When encapsulation efficiency is elevated, it typically indicates that a larger proportion of the drug is securely embedded or confined within the polymer matrix. This confinement can impede the diffusion of the drug, resulting in a reduced release rate. Conversely, when encapsulation efficiency is lower, the drug may be more accessible at the surface or within the more porous areas of the polymer matrix, thereby promoting a more rapid release.
The selection of specific polymers, including PLA, PVP, and the volume of PVA, is critical in determining the properties of the resulting formulations. For example, PLA is characterized by its slow degradation rate and hydrophobic properties, which can improve encapsulation efficiency while simultaneously limiting water penetration and drug diffusion. The interactions and balance between these polymers, along with their respective concentrations, play a crucial role in determining the efficiency of drug encapsulation and the subsequent release mechanisms [
14].
The opposing directions of the objectives indicate a conflict or trade-off between them. Achieving improvement in one objective often leads to deterioration in the other. This conflict arises due to inherent constraints in the system being optimized. In microsphere formulations, increasing the drug release rate may compromise encapsulation efficiency due to the properties of the materials used, such as the polymers. It is well recognized that polymers have a positive effect on enhancing the encapsulation of drugs. On the other hand, polymer complexation can result in increased hardness of the microspheres. Therefore, the drug release may slow down and follow more sustained release patterns [
7]. In pharmaceutical formulations containing candesartan cilexetil, the optimal ranges for encapsulation efficiency and drug release are highly dependent on the specific application. Achieving a higher encapsulation efficiency is crucial for the effective entrapment of the maximum quantity of candesartan cilexetil within the delivery system, which is particularly important for sustained-release formulations. This efficient entrapment reduces drug loss and enhances the stability of the formulation, thereby facilitating a more controlled and gradual release of the drug. Conversely, in cases where rapid drug release is required, the formulation may be adjusted to achieve lower encapsulation efficiency or to incorporate a higher proportion of hydrophilic or biodegradable excipients. Such adjustments facilitate accelerated drug diffusion and absorption. The specific acceptable ranges for encapsulation efficiency and drug release are ultimately dictated by the therapeutic objectives associated with candesartan cilexetil. They must comply with regulatory standards to ensure both safety and efficacy.
c shows the Pareto fronts generated by various MOO algorithms. It can be observed that the Pareto front represents the trade-off between the two objectives. The convex shape of the Pareto front suggests a non-linear relationship between the objectives. This implies that there is no single solution that can simultaneously optimize both objectives to their absolute maximum values. Instead, the Pareto front showcases the best compromise solutions, where improving one objective necessitates sacrificing the other to some extent. This reflects the inherent trade-off nature of the problem.
The algorithms exhibit variations in their ability to explore and converge to diverse regions of the Pareto front. Evaluating these fronts can provide valuable information about the strengths and weaknesses of each algorithm in finding diverse and well-distributed solutions, which is crucial for decision-making in multi-objective optimization problems. Therefore, different performance indicators were applied to evaluate the convergence of algorithms, approximation to the true Pareto-optimal set, and the spread of the solutions.
. Panels (<b>a</b>) and (<b>b</b>) represent the 3D plots for the three variables (PLA, V-PVA, and PVP) as a function of the Encapsulation efficiency and Drug release (Objective 1 and Objective 2), respectively. (<b>c</b>) A representation of the Pareto front for the two objectives.
Multi-objective optimization algorithms play a pivotal role in tackling complex decision-making problems where multiple conflicting objectives need to be optimized simultaneously. In this study, a thorough examination and comparison of five prominent MOO algorithms was conducted across various performance metrics, which are represented in a–f.
Firstly, the hypervolume (Hv) metric serves as a fundamental measure reflecting the spread and diversity of solutions in the Pareto front. Notably, MOEA/D demonstrated the highest Hv value, indicating its ability to generate well-distributed solutions along the Pareto front. Conversely, RVEA and C-TAEA exhibited lower Hv scores, suggesting potential limitations in maintaining diversity within their solution sets. Next, the generational distance (GD) metric evaluates the convergence of solutions to the true Pareto front. NSGA-III and MOEAD outperformed other algorithms in minimizing GD, indicating superior convergence capabilities. However, AGE-MOEA showcased a slightly higher GD, suggesting a trade-off between convergence and diversity. The inverted generational distance (IGD) metric provides insights into the quality of solutions concerning the true Pareto front. Remarkably, MOEA/D achieved the lowest IGD score, highlighting its ability to produce solutions that are closer to the Pareto front. Conversely, RVEA and C-TAEA exhibited relatively higher IGD values, indicating potential challenges in achieving optimal solutions.
Moreover, the spacing metric assesses the evenness of solutions along the Pareto front. MOEAD demonstrated a significantly higher spacing value, indicating a more evenly distributed set of solutions compared to other algorithms. Conversely, C-TAEA exhibited a lower spacing value, implying potential clustering of solutions. Furthermore, the maximum spread metric evaluates the coverage of solutions in the objective space. MOEAD showcased the highest maximum spread, suggesting its effectiveness in exploring a wide range of solutions across the objective space. In contrast, C-TAEA demonstrated a relatively lower maximum spread, indicating potential limitations in exploring diverse regions of the objective space. Lastly, the spread metric evaluates both convergence and diversity aspects. MOEAD exhibited the highest spread metric value, reflecting its balanced performance in achieving both convergence and diversity. Conversely, C-TAEA showcased a slightly lower spread metric, suggesting a potential trade-off between convergence and diversity in its solution set.
. Statistical indicators representing the performance of each multi-objective optimization algorithm. (<b>a</b>) hypervolume, (<b>b</b>) generational distance, (<b>c</b>) inverted generational distance, (<b>d</b>) spacing, (<b>e</b>) maximum spread, and (<b>f</b>) spread metric.
When evaluating multi-objective optimization algorithms, the WSM score provides a valuable metric for comparing the quality of formulations. In this analysis, several prominent MOO algorithms, including NSGA-III, MOEA/D, AGE-MOEA, RVEA, and C-TAEA, were evaluated based on their WSM scores. The aim was to discern which algorithm yielded the most optimal solutions across a set of objectives. Based on the WSM scores resulted, the MOO algorithms can be ranked according to their performance in optimizing the objectives. The higher the WSM score, the better the solution is considered in terms of the weighted sum of objectives.
In this analysis, the performance of various MOO algorithms in balancing formulation quality was explored to achieve high encapsulation efficiency and drug release within 12 h. presents a comparison of MOO algorithms across different formulation factors (Var1 to Var3) and their corresponding objective values, along with their WSM scores. Formulation quality is crucial in pharmaceutical and encapsulation applications. Var1 to Var3 represent various formulation parameters, including PLA, V-PVA, and PVP, which are crucial for determining the characteristics of the encapsulation system. The selection of these variables significantly impacts the encapsulation efficiency and drug release properties, ultimately influencing the effectiveness of the delivery system.
Among the evaluated algorithms, NSGA-III emerged as the top performer, achieving the highest WSM score of 82.0776. This result indicates that NSGA-III consistently generated solutions with the most favorable weighted sum of objective values compared to its counterparts. It suggests robustness and effectiveness in exploring the solution space and achieving a balance between conflicting objectives. Following closely behind NSGA-III, MOEAD secured the second position with a slightly lower WSM score of 80.8869. Although it fell short of NSGA-III’s score, MOEAD demonstrated notable performance in optimizing the objectives. The solutions demonstrated competitive trade-offs among conflicting objectives, emphasizing their effectiveness in multi-objective optimization tasks.
Similarly, AGE-MOEA attained a commendable WSM score of 80.9665, positioning it as another strong contender among the evaluated algorithms. Its ability to produce solutions with high weighted sum values underscores its effectiveness in addressing complex optimization challenges and achieving diverse Pareto-optimal solutions. RVEA and C-TAEA, while still achieving respectable WSM scores of 79.4223 and 79.7074, respectively, exhibited slightly lower performance compared to NSGA-III, MOEAD, and AGE-MOEA. Nonetheless, their scores signify their capability to generate solutions with competitive weighted sum values, albeit with some trade-offs in optimization performance.
The analysis of WSM scores offers valuable insights into the relative performance of MOO algorithms in the context of optimizing a set of objectives. In this evaluation, NSGA-III emerged as the leading performer, while MOEAD and AGE-MOEA also exhibited robust performance. In contrast, RVEA and C-TAEA demonstrated lower WSM scores. The MOO optimization approach shows promise, particularly in optimizing the balance between encapsulation efficiency and release rate at the 12-h mark, with NSGA-III achieving the most favorable results. However, it is noteworthy that, although the MOO algorithms provide comparable predictions for release rates, they exhibit a slight compromise in encapsulation efficiency compared to the optimal formulation suggested in the existing literature [
7]. Further refinement and additional experimental validation are warranted to ascertain the practicality of these optimized formulations in real-world applications.
. Comparison of formulation quality based on WSM scores.
4. Conclusions
This study employs five prominent multi-objective optimization algorithms—NSGA-III, MOEAD, RVEA, C-TAEA, and AGE-MOEA—in conjunction with response surface models to yield significant insights into the formulation quality of candesartan cilexetil microencapsulation. The findings highlight the inherent trade-offs between encapsulation efficiency and drug release, emphasizing the complexity of achieving an optimal balance between these conflicting objectives. This complexity is further illustrated by the non-linear relationships and compromise solutions represented on the Pareto fronts generated by the MOO algorithms.
Each algorithm exhibited distinct strengths in exploring and converging to various regions of the Pareto front. NSGA-III emerged as the most effective in identifying high-quality formulations, while MOEAD and AGE-MOEA also demonstrated commendable performance in balancing competitive trade-offs. Although RVEA and C-TAEA displayed slightly lower overall performance, they nonetheless proved valuable by generating solutions with notable formulation quality. These variations among the algorithms underscore the significance of selecting an appropriate algorithm based on specific optimization objectives and decision-making criteria.
The findings possess significant practical implications for the development of formulations, particularly in informing the design of drug delivery systems that necessitate precise control over encapsulation and release profiles. By understanding the trade-offs between encapsulation efficiency and drug release, formulation scientists are equipped to make informed decisions aimed at optimizing drug bioavailability and therapeutic efficacy. For example, the identified trade-offs are especially significant in developing sustained-release or targeted drug delivery formulations, where achieving the right balance of polymer properties is critical. Future research should investigate the application of these optimization strategies to a wider array of drug candidates and polymer systems, potentially incorporating advanced materials such as nanocarriers or stimuli-responsive polymers. Furthermore, subsequent studies could concentrate on refining response surface models or integrating machine learning techniques to improve prediction accuracy and optimization efficiency. By exploring these avenues, this approach could be further developed to facilitate the creation of more effective and personalized drug delivery solutions.
Acknowledgments
The authors would like to acknowledge the Laboratory of Biomaterials and Transport Phenomena and SAIDAL of Medea.
Author Contributions
Conceptualization, M.K.A. and A.M.; Methodology, M.K.A. and A.M. and F.O.; Software, M.K.A.; Validation, M.K.A. and M.H.; Formal Analysis, M.K.A.; Investigation, M.K.A., F.O., A.M. and M.H.; Writing—Original Draft Preparation, M.K.A.; Writing—Review & Editing, M.K.A.
Ethics Statement
Not applicable.
Informed Consent Statement
Not applicable.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
References
1.
Pereira JLJ, Oliver GA, Francisco MB, Cunha SS, Gomes GF. A
Review
of
Multi-Objective
Optimization:
Methods
and
Algorithms
in
Mechanical
Engineering
Problems.
Arch. Comput. Methods Eng. 2022,
29, 2285–2308. doi:10.1007/s11831-021-09663-x.
[Google Scholar]
2.
Sharma S, Kumar V.
A
Comprehensive
Review
on
Multi-Objective
Optimization
Techniques:
Past,
Present
and
Future.
Arch. Comput. Methods Eng. 2022,
29, 5605–5633. doi:10.1007/s11831-022-09778-9.
[Google Scholar]
3.
Kouider Amar M, Rahal S, Laidi M, Boukessani H, Hallouane H, Kerbouci K, et al. A
Comparative
Study
of
Multi-Objective
Methods
and
Algorithms
for
Optimizing
Emulgels
Consistency
and
Drug
Diffusion.
J. Drug Deliv. Sci. Technol. 2023,
89, 104996. doi:10.1016/j.jddst.2023.104996.
[Google Scholar]
4.
Kouider Amar M, Rahal S, Laidi M, Kouar I, Bourahla RFE-K, Akouche Y, et al. Balancing
Competing
Objectives
in
Bigel
Formulations
Using
Many-Objective
Optimization
Algorithms
and
Different
Decision-Making
Methods.
Eur. J. Pharm. Biopharm. 2024,
195, 114167. doi:10.1016/j.ejpb.2023.12.007.
[Google Scholar]
5.
Premkumar M, Jangir P, Sowmya R, Alhelou HH, Mirjalili S, Kumar BS.
Multi-Objective
Equilibrium
Optimizer:
Framework
and
Development
for
Solving
Multi-Objective
Optimization
Problems.
J. Comput. Des. Eng. 2022,
9, 24–50. doi:10.1093/jcde/qwab065.
[Google Scholar]
6.
Rangaiah GP, Feng Z, Hoadley AF.
Multi-Objective
Optimization
Applications
in
Chemical
Process
Engineering:
Tutorial
and
Review.
Processes 2020,
8, 508.
[Google Scholar]
7.
Chabane A, Bouchal F, Hentabli M, Ayachi N, Slama HE, Rezgui F, et al. Investigation
of
the
Candesartan
Cilexetil
Antihypertensive
Drug
Microencapsulation
by
PLA-PVP
K30
Biodegradable
Polymers:
Experimental
Optimization
and
Release
Kinetics
Modelling.
Can. J. Chem. Eng. 2023,
101, 4446–4459. doi:10.1002/cjce.24811.
[Google Scholar]
8.
Vesikar Y, Deb K, Blank J. Reference Point Based NSGA-III for Preferred Solutions. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1587–1594.
9.
Zhang Q, Li H. MOEA/D:
A
Multiobjective
Evolutionary
Algorithm
Based
on
Decomposition.
IEEE Trans. Evol. Comput. 2007,
11, 712–731. doi:10.1109/TEVC.2007.892759.
[Google Scholar]
10.
Cheng R, Jin Y, Olhofer M, Sendhoff B. A
Reference
Vector
Guided
Evolutionary
Algorithm
for
Many-Objective
Optimization.
IEEE Trans. Evol. Comput. 2016,
20, 773–791. doi:10.1109/TEVC.2016.2519378.
[Google Scholar]
11.
Li K, Chen R, Fu G, Yao X. Two-Archive
Evolutionary
Algorithm
for
Constrained
Multiobjective
Optimization.
IEEE Trans. Evol. Comput. 2019,
23, 303–315. doi:10.1109/TEVC.2018.2855411.
[Google Scholar]
12.
Panichella A. An Adaptive Evolutionary Algorithm Based on Non-Euclidean Geometry for Many-Objective Optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 595–603.
13.
Arbia W, Kouider Amar M, Adour L, Amrane A. Maximizing
Chitin
and
Chitosan
Recovery
Yields
from
Fusarium
Verticillioides
Using
a
Many-Factors-at-a-Time
Approach.
Int. J. Biol. Macromol. 2024,
282, 136708. doi:10.1016/j.ijbiomac.2024.136708.
[Google Scholar]
14.
Farah S, Anderson DG, Langer R. Physical
and
Mechanical
Properties
of
PLA,
and
Their
Functions
in
Widespread
Applications
—A
Comprehensive
Review.
Adv. Drug Deliv. Rev. 2016,
107, 367–392. doi:10.1016/j.addr.2016.06.012.
[Google Scholar]