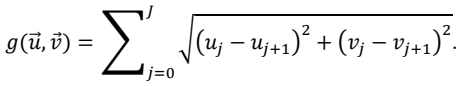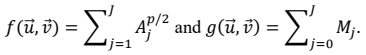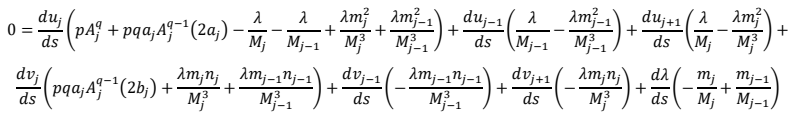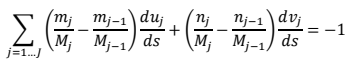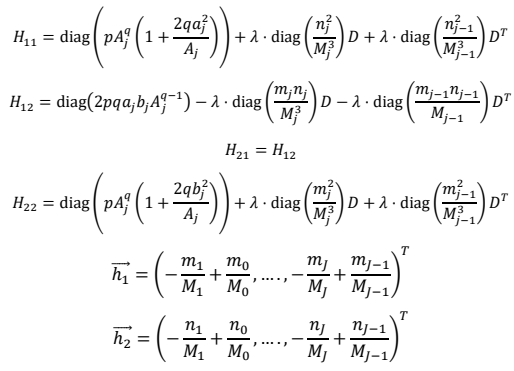2.1. System Assumptions
We consider a remote sensing system that satisfies the following assumptions:
(
A1) The system includes a wireless sensor network with predetermined cluster heads. Each sensor in the field transmits its information (either directly or indirectly) to one of the cluster heads.
(
A2) The system also includes a drone that flies on a specific trajectory (to be determined) so that each cluster head transmits its energy to the drone when it is nearby.
(
A3) The drone’s energy consumption is determined entirely by the length of the drone’s trajectory. (This is the case for example, if the drone flies at a constant velocity, and there is no wind or other conditions that would affect the flight of the drone.)
(
A4) The drone has a fixed maximum path length, which is determined by the energy capacity of the battery and the rate of energy consumption.
(
A5) The drone’s location is approximately constant while receiving information from a particular cluster head. This assumption is satisfied in either of the following scenarios: (a) the information transmission from the cluster head occupies only a brief period of time, so that the distance the drone moves during the transmission period is negligible; or (b) the drone slows, hovers, or lands during transmission, and consumes no energy during the transmission period.
(
A6) The energy expended by the cluster head in information transmission is proportional to the distance between the cluster head and drone raised to a power law exponent.
We also consider two alternative criteria for optimization:
(
O1) Minimize the total energy expended by cluster heads in information transmission.
(
O2) Minimize the maximum energies expended by cluster heads in information transmission.
The choice of suitable optimization criterion will depend on the particular circumstances of the WSN. For example, in a system with many potential alternative cluster heads, then the maximum consumption among cluster heads may be less important than overall power consumption, so criterion
O1 may be appropriate. On the other hand, if there are few choices for cluster head, then the cluster head with maximum energy expended will need frequent replacement, so criterion
O2 may be a better option. We note that other criteria besides
O1 and
O2 are possible, with minimal changes to the solution, as we indicate in Section 5.
Under assumptions (
A1)–(
A6) and criteria (
O1)–(
O2), it follows that an optimum path for the drone will consist of straight-line segments joining the drones’ locations where it harvests energy from the different cluster heads. This conclusion is reflected in the mathematical description in subsequent sections.
2.2. System Parameters and Variables
The system parameters include:
- (xj, yj), j = 1...J: positions of the cluster heads that are sending the information;
- L: Maximum path length for the drone;
- p: Power loss exponent.
The system variables include:
- (uj,vj), j = 1...J : Drone positions for harvesting information from cluster heads. Here, the order of points the drone takes is assumed to be (uj,vj) to (uj+1,vj+1) for j = 1 ...J − 1.
- (u0,v0), (uJ+1,vJ+1): Drone starting and ending position, respectively.
2.3. Mathematical Formulation of the Optimization Problem
Information transmission from cluster head (
xj,
yj) takes place when the drone is at position (
uj,
vj). The total energy consumption required for information transfer is the sum of the energies from the J cluster heads, which following assumption (
A6), can be represented as a function $$f(\vec{u},\vec{v}){:}$$
where $$\vec{u}:=\begin{bmatrix}u_1,....u_J\end{bmatrix}$$ and $$\vec{v}:=\begin{bmatrix}v_1,....v_J\end{bmatrix}$$.
The distance the drone travels is given by $$g(\vec{u},\vec{v})$$, where
The drone’s limited range imposes the constraint $$g(\vec{u},\vec{v})$$ ≤
L, where
L is the maximum distance the drone can travel. In the case where
L is large enough so that the drone is capable of making a complete tour of the cluster heads, then any such complete tour will give $$g(\vec{u},\vec{v})$$ = 0 and is thus an optimal solution to the problem. So we consider instead the more difficult problem where
L is smaller than the smallest tour distance, so $$g(\vec{u},\vec{v})$$ = 0 is impossible. In this case, we may replace the inequality with an equality constraint. This can be seen as follows. Suppose a drone path includes the point (
uj,
vj) where $$|(u_j,v_j)-(x_j,y_j)|>0.$$ For simplicity, we define:
Then, for any δ with 0 < δ ≤ 1, we have
so replacing $$\vec{w}_{j}$$ with $$\vec{w}_{j}+\delta(\vec{z}_{j}-\vec{w}_{j})$$ will reduce the energy function (1). Now, if the drone path length is less than
L, then
δ > 0 can be chosen sufficiently small such that replacing $$\vec{w}_{j}$$ with $$\vec{w}_{j}+\delta(\vec{z}_{j}-\vec{w}_{j})$$ still yields total drone path length of less than
L. Thus, any drone path with a length less than
L can be improved—so no drone path with a length less than
L can be optimal.
We may now formulate the optimization problem. In case (
O1), we have
In case (
O2), minimizing the maximum transmission energy is equivalent to minimizing $$|\vec{w}_{j}-\vec{z}_{j}|$$ over all
j. Using the equality
with $$a_{j}:=|\vec{w}_{j}-\vec{z}_{j}|$$, we conclude that by taking
p sufficiently large, we can approach the solution to (
O2) with arbitrary precision.
2.4. Local Optimization Conditions
The minimization problem (5) leads to the following Lagrange multiplier condition for a local minimum:
where ∇
h denotes the gradient of
h with respect to $$(\vec{u},\vec{v})$$:
and
λ is a Lagrange multiplier.
Writing the vector Equation (7) out in terms of components, we have:
For notational simplicity, we define new variables. For
j = 1….
J, let
Then we have:
Using this notation, we have:
where $$q{:}=\frac{p}{2}-1$$, and
Similarly, we have:
It follows that we may rewrite the equations in (9) as:
Equations (16) are required for local optimality and are necessary for global optimality but not sufficient. Thus, the solutions that we provide in this paper may not be optimal for all global situations. We return to this issue in Section 2.8.
2.5. Homotopy Approach to Local Optimization for a Given Path Length
Solutions of the fundamental optimization problem (5) for different values of
L correspond to solutions of (16) with different values of
λ. As
L is varied continuously, the value of
λ will also vary continuously, and the components of $$\vec{u}$$ and $$\vec{v}$$ will vary continuously as well. This suggests that if we have a solution to (5) for a given value of
L, we may be able to perturb that solution differentially to obtain solutions for different values of
L. In fact, we do have a solution for a particular value of
L: namely
f( $$\vec{u}$$, $$\vec{v}$$) = 0 when
uj =
xj and
vj =
yj, which solves the constraint $$g(\vec{u},\vec{v})$$ =
L when
L is equal to the length of the tour that connects the points $$({\vec{x}}_{j},{\vec{y}}_{j})$$ in consecutive order. The smallest value of
L for this type of solution occurs when the points $$({\vec{x}}_{j},{\vec{y}}_{j})$$ are ordered so that $$(u_{0},v_{0}),(x_{1},y_{1}),(x_{2},y_{2}),...(x_{J},y_{J}),(u_{J+1},v_{J+1})$$ forms a “travelling salesman” tour that connects all points $$({\vec{x}}_{j},{\vec{y}}_{j})$$ with the smallest possible total length.
In practice, we want to find solutions corresponding to
L values that are smaller than the length of a full tour. So we start with the full tour and successively “nudge” the solutions so they correspond to smaller and smaller values of
L. This is an example of a
homotopy approach: start with a solution that is optimal for a different set of conditions and generate a smooth curve of solutions that joins this solution to a solution that satisfies desired conditions. In practice, this smooth curve of solutions is often specified parametrically as the solution to a set of ordinary differential equations. In the next section, we will derive differential equations that can be used to find the parametrized curve that leads to our desired optimal solution.
2.6. Derivation of Differential Equations for Parametrized Homotopy Curve
First, we parametrize solutions to (16) using the parameter s, so that
aj,
bj,
Aj,
mj,
Mj, and λ are all functions of
s. As
s changes, the equalities cannot change, so we have
Since we want to find solutions for smaller values of
L, we want to ensure that
L decreases as
s increases. We may ensure this by adding the condition:
Recall that the variables
aj,
bj,
Aj,
mj,
Mj, in (17) are all functions of $$\vec{u}$$ and $$\vec{v}$$, so the derivatives in (17) can all be expressed in terms of the derivatives $$\frac{du_{j}}{ds}$$ and $$\frac{dv_{j}}{ds}$$ for
j = 1,…..
J. As a result, we obtain a system of 2
J + 1 differential equations for the variables {
uj,
vj},
j = 1….
J and λ.
We may rewrite the first equation in (17) as (
j = 1….
J):
The derivatives in (19) may be expressed in terms of { $$\frac{du_k}{ds}$$} and { $$\frac{dv_j}{ds}$$} using the formulas (
j = 0…..
J):
It follows that (19) with index
j will depend on the derivatives $$\frac{du_k}{ds}$$, $$\frac{dv_k}{ds}$$ and $$\frac{dλ}{ds}$$ for
k =
j $$-$$
1,
j,
j + 1 (noting that $${\frac{du_{0}}{ds}}={\frac{dv_{0}}{ds}}={\frac{du_{j+1}}{ds}}={\frac{dv_{j+1}}{ds}}=0$$. By collecting terms corresponding to each derivative, we find (
j = 1…..
J)
Using various algebraic manipulations and the fact that:
The Equations (19) may be simplified to:
The
J equations associated with the second equation in (17) may be obtained from (23) by exchanging $$u_{k}\leftrightarrow v_{k}$$, $$a_{k}\leftrightarrow b_{k}$$, and $$m_{k}\leftrightarrow n_{k}$$.
Finally, (18) can be expressed in terms of derivatives of {
uj,
vj} as:
The entire system of 2
J +1 equations can be represented in matrix form as:
where
H is a (2
J + 1) × (2
J + 1) matrix, and
u,
z are column vectors of length 2
J + 1, given by the formulas:
(i.e.,
z has a single nonzero entry of −1 in the last component). The matrix
H can be decomposed into blocks:
The blocks
Hij can be expressed in terms of diagonal and subdiagonal matrices. First, we introduce some abbreviated notations. Let diag(
cj) denote the
J ×
J diagonal matrix with entries
c1,...
cJ on the diagonal; and let
D denote the discrete forward derivative matrix with −1’s on the diagonal and 1’s on the first superdiagonal. Then we have:
2.7. Initial Conditions for Differential Equation
In Section 2.5, we suggested that by starting with a complete tour by the drone that visits all sensors and “nudging” the drone’s path, we can find optimal solutions for shorter and shorter path lengths. Unfortunately, the matrix
H in (25) is singular when $$(u_{j},v_{j})=(x_{j},y_{j}),j=1....J$$, which corresponds exactly to the case of a complete tour. So, we cannot use this solution as an initial condition. Fortunately, we can address this problem by choosing a solution where the (
uj,
vj) is slightly offset from (
xj,
yj) for all
j, i.e.,
We need to choose the { $$\vec{\epsilon}_{J}$$ } in such a way that the Lagrange multiplier conditions (7) are satisfied. We also need to choose { $$\vec{\epsilon}_{J}$$} such that the path joining the {(
uj,
vj)} is smaller than the full tour.
The gradient of
f($$\vec{u},\vec{v}$$) evaluated at the point for the initial point given by (29) is given by:
where $$\widehat{\epsilon}_{J}$$ is the unit vector in the direction of $$\vec{\epsilon}$$. The Lagrange multiplier condition (7) gives:
where
Since $$g(\vec{u},\vec{v})$$ is smooth in the vicinity of $$(\vec{u},\vec{v})\approx(\vec{x},\vec{y})$$, we may approximate:
Which may be evaluated using (14) and (15). Denoting the right-hand side of (33) as $$\vec{g_{J}}$$, we have from (31)
Since we are interested in solutions for which g is reduced, we choose the negative sign in (34). Then $$\vec{\epsilon}_{J}$$ is uniquely determined by the values of $$\vec{g_{J}}$$ and λ. By choosing a small value of λ, we may obtain initial values for $$(\vec{u},\vec{v})$$ that are very close to $$(\vec{x},\vec{y})$$, so that the approximation in (33) holds a very high degree of accuracy. In this way, we obtain initial conditions for our differential Equation (25) for which
H is not singular and can then apply standard numerical methods for solution.
2.8. Global Optimality for Sufficiently Long Drone Ranges
In Section 2.4, we posed the local optimality condition (7) from which the vector differential Equation (25) is derived. To show that a locally optimal solution is globally optimal, we would need to show that it improves over all other locally optimal solutions. We may establish this for the solutions described in Sections 2.5–2.7 for drone ranges that are less than but close to the travelling salesman tour length as follows. Here we give a brief outline of the proof; a more extended presentation is given in Appendix B.
Every local optimal solution for a given drone path length will be part of a homotopy of solutions that may be parametrized by path length. As path length increases in the homotopy, the energy consumption decreases until a minimum energy consumption is reached for the entire homotopy. This minimum energy is necessarily nonnegative—and if it is 0, then the homotopy must terminate at a tour that joins all of the cluster heads. The shortest cluster head tour (i.e., the travelling salesman solution) will be the unique optimum in the case when the drone path length is equal to this shortest tour. It follows that for sufficiently long drone path lengths, the solution that belongs to the homotopy that includes the travelling salesman solution will be the unique global optimum. This justifies our claim that the solution of (5) calculated using the homotopy approach outlined in Sections 2.5–2.7 is optimal for sufficiently long drone ranges.
The limited nature of this proof does not necessarily mean that the solution we have presented is not globally optimal for shorter drone ranges: global optimality is notoriously difficult to establish rigorously, except in the case where the function to be optimized has nice properties such as convexity. Nonetheless, the proof adds credibility to the expectation that the obtained solution has a strong likelihood of being not just locally optimal but also globally optimal.
2.9. Implementation in Python
As described above, the algorithm has two phases. First, an initial ordering of cluster heads is determined, such that the length of a tour joining the cluster heads in this order is minimized among all possible orderings. Once the ordering is set, the homotopy of solutions is computed using the initial conditions and system of differential equations described in Sections 2.7 and 2.5. The final path with the desired path length is selected from the homotopy.
For the first phase, the shortest tour joining cluster heads is found using the travelling salesman algorithm as implemented in the python-tsp package. This gives a set of ordered cluster head points, that is, (
xj,
yj) re-arranged appropriately.
For the second phase, the homotopy solution is computed according to the following steps:
Step 0: Initialize cluster head locations, initial value of λ, and step size h (typically on the order of 0.1),
Step 1: Find a minimal initial path joining the cluster head points using a travelling salesman algorithm.
Step 2: Determine the initial points of the closest approach to be a small distance away from the cluster head points, according to the algorithm described in Section 2.7.
Step 3: Solve the homotopy Equations (25) numerically. Initially, we used the odeint solver from the scipy package but encountered instabilities when the path vertices began to merge. We succeeded better using a Runge Kutta-4 code obtained from the web and modified for our purpose.
Appendix A gives a more detailed description of the code as well as a link to a Github page where the code can be downloaded.
2.10. Specification of Test Cases
The Python implementation of the algorithm was tested by simulating a number of different cluster head configurations, with various numbers of cluster heads and drone starting positions. The test configurations used have the following cluster head position:
Case 1: [(2, 1), (2, 4), (6, 4), (6, 1)]
Case 2: [(2, 1), (2, 4), (8, 2), (6, 4), (6, 1)]
Case 3: [(2, 1), (2, 4), (8, 2), (6, 4), (6, 1)]
Case 4: [(2, 1), (2, 4), (8, 2), (6, 4), (6, 1), (7, 3.5), (1, 2.5)]
Case 5: [(2,1), (2, 4), (8, 2), (6, 4), (6, 1), (7, 3.5), (1, 2.5), (3,6)]
Case 6: [(2,1), (2, 4), (8, 2), (6, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5)]
Case 7: [(0.5,1), (2, 4), (8, 2), (9, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5),(7.5,6), (4,8.5), (5.5,10)]
Case 8: [(0.5,1), (2, 4), (8, 2), (9, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5),(7.5,6), (4,8.5), (5.5,10), (3.5,12)]
Case 9: [(0.5,1), (2, 4), (8, 2), (9, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5),(7.5,6), (4,8.5), (5.5,10), (3.5,12), (2.25,10)]
Case 10: [(0.5,1), (2, 4), (8, 2), (9, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5),(7.5,6), (4,8.5), (5.5,10), (3.5,12), (2.25,10), (6.25,16)]
Case 11: [(0.5,1), (2, 4), (8, 2), (9, 4), (6.5, 1.5), (7, 3.5), (1, 2.5), (3,6), (3,1), (5,0.5),(7.5,6), (4,8.5), (5.5,10), (3.5,12), (2.25,10), (6.25,16), (7,11)]
These configurations were chosen manually so as to have homotopy solutions that are easily visible as well as to be sufficiently similar so that trends in the homotopy as the number of points increases are also visible. All cases used a transmission power loss exponent of 2, with the finishing position of drone equal to (0,0). The drone path starting point is (0,0), except for Case 3 in which the starting point is (3,1). For each configuration, the travelling salesman tour was computed, as well as the homotopy of solutions obtained when the drone path length
L is decreased from the travelling salesman tour length down to the minimum path joining the tour starting and ending point. A step size of 0.1 was used for the numerical solution for all cases.
The solution described above for finding optimal drone information-harvesting paths is locally and globally optimal for sufficiently long drone ranges. The numerical solution algorithm executes quickly enough that it can be implemented in real-time, and execution time grows slowly with the size of the system. The solution can be used either to optimize total transmit power consumption and maximum power consumption by cluster heads. However, there are limitations in that the speed of execution slows considerably when the drone range decreases below a certain point (i.e., when path vertices begin to merge), and global optimality for comparatively short drone ranges is uncertain.
In this appendix, we give a more extended presentation of the argument outlined in Section 2.8, which asserts that the homotopy solution found in Sections 2.5–2.7 is a globally optimal solution of (5) for drone ranges that are less than but close to the travelling salesman tour length. A completely rigorous mathematical argument would be tedious to present, but a step-by-step outline is as follows.
Suppose first we restrict to drone path solutions such that (uj,vj) is in the same order of (xj,yj ), j = 1,…J where (xj,yj) is the travelling salesman order of cluster heads. Suppose also that $$\left(\vec{u}^{(ts)}(L),\vec{v}^{(ts)}(L)\right)$$ is a globally optimal solution for the drone path satisfying the constraint $$g\big(\vec{u}^{(ts)}(L),\vec{v}^{(ts)}(L)\big)$$ = L. Any globally optimal solution of (5) is also locally optimal: so $$\left(\vec{u}^{(ts)}(L),\vec{v}^{(ts)}(L)\right)$$ is also locally optimal. Then $$\left(\vec{u}^{(ts)}(L),\vec{v}^{(ts)}(L)\right)$$ is part of a homotopy of solutions using the same construction we showed in Sections 2.5–2.7. The homotopy consists of locally optimal solutions $$\left(\vec{u}^{(ts)}(s),\vec{v}^{(ts)}(s)\right)$$ satisfying $$g\big(\vec{u}^{(ts)}(s),\vec{v}^{(ts)}(s)\big)$$ = s, where s can take values in a closed interval containing L. Define the function $$f_{(ts)}(s)=f\big(\vec{u}^{(ts)}(s),\vec{v}^{(ts)}(s)\big)$$. The function f(ts) decreases strictly as s increases, because if the drone path is lengthened, it is always possible to move closer to the cluster heads; and as long as f(ts) (s) is positive, it is always possible to decrease fI by increasing the path length. It follows that the minimum value of f(ts) (s) on the homotopy cannot be positive, so $$\left(\vec{u}^{(ts)}(L),\vec{v}^{(ts)}(L)\right)$$ must be connected by a homotopy to ( $$\vec{x},\vec{y}$$) where the components of $$\vec{x}$$ and $$\vec{y}$$ are in travelling salesman order. So the solution in this homotopy whose length is equal to the travelling salesman tour length of cluster heads (denoted by $$L^{(ts)}$$) corresponds to a value of $$f_{(ts)}\big(L^{(ts)}\big)$$ = 0.
Now, we consider solutions where (uj,vj ) receives the information from $$(x_{\sigma(j)},y_{\sigma(j)})$$ where σ is a permutation of (1,…J). By similar arguments as in the previous paragraph, any locally optimal solution corresponding to a path length L is part of a homotopy $$\left(\vec{u}^{(\sigma)}(s),\vec{v}^{(\sigma)}(s)\right)$$ with associated strictly decreasing function $$f_{\sigma}(s):=f\big(\vec{u}_{\sigma}(s),\vec{v}_{\sigma}(s)\big)$$, which includes a solution $$\left(\vec{u}^{(\sigma)}\big(L^{(\sigma)}\big),\vec{v}^{(\sigma)}\big(L^{(\sigma)}\big)\right)$$ for path length $$L^{(\sigma)}>L$$ such that $$f_{\sigma}\big(L^{(\sigma)}\big)=0$$. But this implies that $$\left(\vec{u}^{(\sigma)}\big(L^{(\sigma)}\big)_{j^{\prime}},\vec{v}^{(\sigma)}\big(L^{(\sigma)}\big)_{j}\right)=\big(x_{\sigma(j)},y_{\sigma(j)}\big)$$,j = 1,…J, which in turn implies that $$L^{(\sigma)}$$ is the length of the tour of the points $$\left\{\left(x_{j},y_{j}\right)\right\}_{j=1...J}$$ in the order given by σ. This means that $$L^{(\sigma)}\geq L^{(ts)}$$, and $$L^{(\sigma)}=L^{(ts)}$$ if and only if σ gives a travelling salesman ordering of the nodes in $$\vec{x},\vec{y}$$. Since the function fσ(s) is strictly decreasing, it follows that $$f_\sigma(L^{(ts)})$$ > $$f_{opt}(L^{(ts)}$$ for all permutations σ for which $$(x_{\sigma(j)},y_{\sigma(j)})$$ is not a travelling salesman permutation. Let $$\tilde{f}:=\min_{\sigma\neq I}f_\sigma $$, where the minimum is taken over all non-travelling salesman permutations. Then we also have $$\tilde{f}\big(L^{(ts)}\big)>f_{(ts)}(L^{(ts)})$$. It follows by continuity that there is an $$\tilde{L}$$ with 0 < $$\tilde{L}$$ < $$L^{(ts)}$$ such that $$\tilde{f}(s)>f_{(ts)}(s)$$ for $$\tilde{L}\leq s\leq L$$. In other words, the solution $$\begin{pmatrix}\vec{u}^{(I)}(s),\vec{v}^{(I)}(s)\end{pmatrix}$$ is a local optimum such that $$f\left(\vec{u}^{(I)}(s),\vec{v}^{(I)}(s)\right)$$ is less than the value of f for any other local optimum. It follows that $$\left(\vec{u}^{(ts)}(s),\vec{v}^{(ts)}(s)\right)$$ is a global optimum for $$\tilde{L}$$ < s $$\leq L^{(ts)}$$.
Note that this proof does not give a practical, constructive method for finding $$\tilde{L}$$ it only shows that it exists. However, the proof does indicate that any global optimum will be part of some homotopy that includes the points {(xj,yj)},j = 1…J in some order. This fact indicates that other candidate global optimal solutions can be found by creating homotopies starting from other (non-travelling salesman) tours of the cluster heads points.
The authors wish to thank Dr. Aristide Tsemo for his thorough review of the equations in Section 2.6, which resulted in several corrections. We also wish to thank the reviewers of this paper, who made several valuable suggestions for improvements.
Conceptualization, R.G. and C.T.; Methodology, R.G. and C.T.; Software, R.G.; Validation, R.G. and C.T.; Formal Analysis, R.G. and C.T.; Investigation, R.G. and C.T.; Writing—Original Draft Preparation, R.G. and C.T.; Writing—Review & Editing, R.G. and C.T.; Visualization, R.G. and C.T.; Supervision, C.T.
Not applicable.
Not applicable.
This research received no external funding.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.