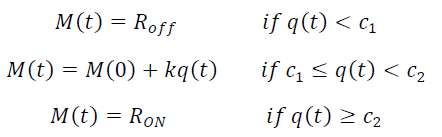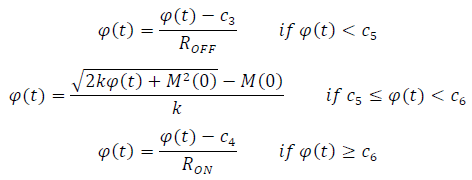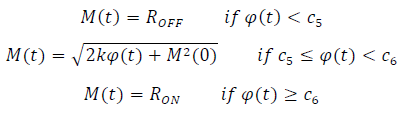1. Introduction
Unmanned Aerial Vehicles (UAVs), better known as drones, are among the most developed and innovative robotic devices in recent years. Their high versatility for outdoor potential applications in agriculture [
1,
2], disaster management [
3,
4], defence [
5,
6], construction [
7], transportation [
8], and infrastructure inspection [
9,
10], or indoor such inventory management in warehouses [
11], among others, has led to their exponential increase in use. In the past, most of the aforementioned applications required the use of aeroplanes or helicopters, which presented several significant disadvantages, including: (1) high operational and deployment costs, (2) high levels of pollution, and (3) the need for onboard crew. For these reasons, UAVs have become valuable tools, addressing these drawbacks by offering low maintenance requirements, eliminating the need for fossil fuels, and providing the capability for remote operation or autonomous functioning.
Both remote and autonomous operations require various essential modules for proper execution. One of the most critical modules is localization, whose function is to estimate the spatial position and orientation based on some form of environmental perception. One of the most common approaches to address this problem is through sensor fusion algorithms, such as Extended Kalman Filters (EKF) [
12] or Particle Filters (PF) [
13]. However, EKF suffers from low efficiency and data-related problems, as well as difficulties in producing large-scale maps. [
14]. The PFs, on the other hand, have a higher computational cost compared to the EKF calculations, which are less time-consuming [
15]. Another widely used approach for UAV localization is based on visual information [
16,
17]. However, in these cases, there is a very strong dependency between the camera calibration and the accuracy of the pose estimations [
18]. This calibration process also introduces a hardware model dependency. Additionally, another disadvantage is the requirement for the presence of distinguishable objects in the environment, allowing for the detection and tracking of features in images captured at consecutive time instances to predict the UAV’s pose [
19]. This dependency becomes problematic in repetitive environments, such as vast plains or fields lacking multiple objects that can be used to track features or differentiate one perception from another [
20]. As a result, these types of solutions tend to accumulate increasing errors in their estimations. Consequently, there is a dependence on the environment that limits the applicability of these algorithms in autonomous robotic systems. The search for alternatives to overcome the disadvantages mentioned above led to the exploration of pose estimation methods inspired by biological organisms, giving rise to bioinspired localization algorithms [
21].
Real-Time Kinematic (RTK) is another widely used method for UAV localization [
22,
23]. It is a high-precision localization method, generally in the range of centimeters. This system uses signals of Global Positioning System (GPS) or Global Navigation Satellite System (GLONASS) in real time. The principle of RTK positioning [
24] consists in comparing two stations called base and mobile. The first, located at a known position, receives satellite signals, calculates its own position and then transmits the corrections in real time. The second, located on the UAV, receives the satellite signals and the corrections sent by the base station to calculate its exact position with much higher accuracy than traditional GPS. While the RTK system provides an accurate and stable position in real time, its main disadvantage is the need for two bases and its high cost compared to other forms of UAV localization.
Biologically, Neuroscience has demonstrated, through the analysis of the brains of rodents and other mammals, the existence of certain brain regions that, based on environmental perceptions provided by the five senses, either individually or combined, using for example, vision alone or vision and touch, are responsible for estimating the orientation and spatial location of the animal [
25,
26,
27]. Additionally, these regions inherently can recognize previously visited places, closing the loop when the animal returns to a familiar area. All these extremely attractive and desired characteristics in localization systems allow for maintaining estimation errors within an acceptable threshold for robotic operations. These have been achieved with the development of the bioinspired algorithm known as Rat-SLAM [
28]. It consists of three modules: Experience Map (EM), Pose Cells (PC), and Local View Cells (LVC). Our work obtained the required environmental information from monocular grayscale images and estimates of linear and angular speeds. This Rat-SLAM algorithm, as described, has been used to solve the localization of robots in aerial [
29] and terrestrial [
28] environments, demonstrating promising results.
However, despite its bio-inspired origins, the Rat-SLAM algorithm utilizes three-dimensional arrays in which each cell stores a value corresponding to the state of a neuron. Consequently, it cannot process information like the biological brain. In the latter, neuronal activity is governed by asynchronous electrical impulses driven by electrochemical processes. This type of processing, based on discrete and asynchronous spike trains, is computationally less expensive than the synchronous floating-point number packages used in classical Artificial Neural Networks (ANNs) in Artificial Intelligence (AI) [
30]. This significant advantage inspired the development of Spiking Neural Networks (SNN) [
31], where information is encoded in the timing or frequency of the spikes. Consequently, neurons must be modelled to replicate biological behaviour. A compelling way to achieve this, particularly from an energy consumption standpoint, is through the development of specialized hardware known as Neuromorphic Computing (NC) [
32]. This discipline focuses on modelling biological structures with electronic circuits. One example of such circuits is the parallel RC circuit, which models the Leaky Integrate-and-Fire (LIF) neuron [
33]. However, the emergence of the memristor as the fourth fundamental element in electronics [
34] allows the replacement of the resistor with a memristor in the aforementioned neuronal model. This substitution incorporates the memristor’s intrinsic memory and low-power properties, giving rise to the Memristive Leaky Integrate-and-Fire (MLIF) model [
35].
In this work, we develop an MLIF-based RatSLAM algorithm to address the 4DoF localization of UAVs. Our proposal includes, on one hand, the incorporation of the MLIF model in the central module of the Rat-SLAM algorithm to represent the Pose Cells (PC), which is a clear application case of Neuromorphic Computing (NC). Thus, we will refer to the resulting PCs as PC-MLIF. These exhibit information processing capabilities closer to biological systems, with neurons that integrate the intrinsic properties of the memristor and the potential for implementation in hardware devices. On the other hand, since our goal is to apply this algorithm in aerial environments, it is essential to estimate at least four variables that define the localization. These are the 3D spatial location and the orientation (yaw).
Motivated by the exploration and analysis of the benefits of UAV navigation using bio-inspired systems, we propose a Rat-SLAM system that encodes spatial localization and orientation at the neuronal level in two PC-MLIF networks. In the latter, we propose to use the MLIF neuron model from NC to process information in a way that is closer to biological systems. The validation of this hypothesis would allow us, in future work, to implement the PC-MLIFs in hardware, thereby reducing the onboard computational capacity required for the localization software. In addition, the use of memristors in the MLIF model allows a reduction in power consumption. These two important features make it possible to extend mission duration, a critical factor in the field of autonomous mobile robotics. The contributions of our work are as follows: (1) UAV localization resolution using a modified Rat-SLAM algorithm. This modification involves the implementation of PC-MLIF using the Spiking MLIF neuron model. (2) Encoding UAV poses into spike frequencies or timings. (3) Validate the feasibility of implementing PC-MLIF on a hardware device to improve the energy efficiency of the positioning system. (4) Provide two PC-MLIF networks with intrinsic memory, associating the excitation level of each neuron with a specific UAV pose.
This work is organized as follows: in Section 2, we will conduct a review of the works that inspired us to develop our proposal. In Section 3, we will describe the various methodologies supporting our research. In Section 4, we will explain our Rat-SLAM proposal for aerial environments. Finally, the experimental tests, results discussion, and conclusions will be presented in Sections 5, 6, and 7, respectively.
2. Related Works
Probabilistic approaches are popular for solving localization problems. The EKF is one of the most widely used, as proposed by Cheng et al. [
36]. It is a navigation and landing scheme for a UAV that allows it to autonomously land on an Unmanned Ground Vehicle (UGV) moving in GPS denied environments, using vision, Ultra WideBand (UWB) technology and system information. In the approach phase, they propose an effective Multi-Innovation Forgetting Gradient (MIFG) algorithm to estimate the UAV’s position relative to the target. They then use these estimates to develop a navigation controller that allows the UAV to approach the target and ensures that the UGV enters the field of view of the UAV’s camera. They propose a sensor fusion estimation algorithm based on EKF to achieve precise landing. They validate this with a numerical example and a real experiment, which show promising results. This type of localization, unlike previous proposals, is useful for intelligent UAV-based inspection in extremely confined environments, as proposed in [
37]. In these scenarios, GPS-based positioning is impossible, which is why UWB-based technology is a good solution. However, due to changing conditions, fluctuations in localization performance can lead to UAV instability. The authors propose a high-precision positioning system for UAVs integrating IMU and UWB with an Adaptive EKF (AEKF). Compared to the traditional EKF-based approach, the noise covariance is estimated and controlled to improve performance. Experimental results from simulations and experiments in extremely confined environments show the authors’ algorithm can significantly improve position update rates, as concluded based on position error analysis. However, truncation errors and the Non-Line-Of-Sight (NLOS) errors contribute to degraded positioning accuracy [
38].
Mao et al. [
39] suggest using EKF in outdoor multi-robot systems. They suggest that some miniaturized UAVs rely entirely on the GPS for navigation. In an interference-free environment, GPS signal interruptions of seconds to minutes are common. For UAVs relying on GPS, such an event can be catastrophic. They propose an EKF-based approach to estimating position when the GPS link is lost, using distance measurements between UAVs. A test with three UAVs shows that their position can be determined with an accuracy of up to 40 m from its real position after losing the GPS signal during manoeuvres. This is done by measuring the distance to two other UAVs. However, this type of proposal requires several UAVs, making it impossible to apply to a single robot.
Despite the promising results of the localization solutions, instabilities have been observed during UAV flights, which add to the disadvantage. These instabilities are investigated in [
40], where it is argued that the problem manifests itself as unexpected oscillations that can lead to emergency landings. The analysis focuses on delays in the EKF algorithm used to estimate the UAV’s attitude, position, and velocity. These delays disrupt the flight stabilization process for two main reasons. Perturbations in the magnetic field generated by the UAV’s motors and external magnetic fields, such as those from power lines, can interfere with magnetometer readings, slowing EKF computations. The EKF fusion stage, which combines magnetometer readings with other sensor measurements, can be computationally expensive when dealing with inconsistent magnetic field readings. The authors use the PX4-ECL library [
41] to analyze this second cause, arguing that it increases EKF processing time. They propose moving magnetic field estimation calculations to a separate thread to prevent blocking of the main EKF loop and causing delays. The monitoring techniques implemented allow continuous real-time observation of the system’s behavior. The authors argue that this would prevent them from blocking the EKF’s main loop and causing delays.
Another widespread probabilistic method, to address the localization problem, is the PF. For the position estimation of a UAV, Mraz et al. [
42] propose a highly compact, lightweight, and robust indoor localization method that can run at high frequencies on the UAV’s on-board computer, based on a fusion of camera information and fiducial detection. The PF is implemented in a way that can handle sensor failures and disconnections without issues. Furthermore, it can be extended to include additional sensor inputs. The authors validate their proposal with UAV flight test data in real-world situations, achieving an average position error of less than 0.4 m. Another localization method for UAVs that can be addressed using PF is remote or cooperative localization. In this technique, anchors or beacons, equipped with GPS or UWB, collect information from unknown nodes to estimate their position. Sometimes, these unknown nodes also cooperate and share position information [
43]. Khalaf-Allah [
44] uses this method to address 3D positioning based on Time Difference of Arrival (TDoA) with four anchors using the PF. This approach uses 1000 particles to represent the probability density function (PDF) of interest,
i.e., the posterior PDF of the target node’s position. It uses a resampling procedure to generate particles in the prediction stage, and TDoA measurements determine the weight of each particle, allowing for updating the posterior PDF and estimating the target node’s position. Simulation results demonstrate the approach’s feasibility and its potential for use in indoor positioning applications using UWB wireless technology. The author demonstrates the feasibility of this approach and its potential for use in indoor positioning applications, such as inventory management in large warehouses.
The performance of the two types of filters and two variants of the Kalman filter for localization applications is analyzed in [
45]. The authors conclude that the EKF is a widely used estimation method in autonomous navigation systems, but is characterized by cumulative errors due to the approximate linearization of the system dynamics. On the other hand, the PF does not make assumptions about the shapes of the PDF of the state vector and the measurements. It uses a set of weighted particles to approximate the posterior distribution of the state vector. To achieve convergence, a resampling procedure is performed at each iteration, where particles with low weights are replaced by particles with high weights. PF is suitable for non-Gaussian measurements and provides reliable solutions for nonlinear estimation and control problems. This filter doesn’t require prior knowledge of the statistical properties of the measurements and the system state variables. However, as explained in [
46], two problems often arise during the particle updating stage: particle impoverishment and sample size dependence, which can reduce the precision of the estimation results.
Computer vision has led to better localization methods that address previous solutions’ drawbacks. Li et al. [
47] present a method for relative UAV positioning and target tracking based on a Visual Simultaneous Localization and Mapping (VSLAM) framework. They integrate a neural network for object detection into the VSLAM framework. This method detects moving objects and reconstructs a 3D map of the environment from image sequences. For multi-object tracking, they combine semantic box detection, region matching, and optical flow point matching to perform dynamic object association. The authors assert that this joint association strategy can prevent tracking loss due to the small size of the object in the image sequence. They recover height data based on a plane estimation approach using RANSAC [
48] to address the lack of scale information in the VSLAM system. The proposed method is tested on a UAV dataset created by the authors and a public dataset, demonstrating the solution’s effectiveness for UAV flights. Another localization method uses optical flow as proposed in [
16]. Here, a method is presented to control the 6-DoF of a UAV without an external reference system, allowing fully autonomous flight. The 2D positioning uses the optical flow principle. It uses altitude estimations from ultrasonic, infrared, inertial, and pressure sensors. This helps calculate, control and guide the UAV’s 3D position. All data is processed on the UAV. An external computer with a route planning interface is used for commands. The evaluation shows that the position error is 10 cm in static flight and 30 cm after landing. A VSLAM proposal integrating measurements from multiple cameras to achieve robust position tracking in complex environments is presented in [
17]. The authors analyze iterative optimizations for position tracking and map refinement when using multiple cameras, ensuring accuracy. They extend the PTAM system [
49] to use two cameras with non-overlapping fields of view. The resulting VSLAM system enables autonomous navigation of a MAV in complex scenarios. For operations in large environments, the system is modified to provide visual odometry with constant time. To form a complete VSLAM system, they implement an efficient back-end for loop closure. The back-end maintains a global map based on keyframes, which is also used for loop closure detection. They propose a pose graph optimization method with an adaptive window to refine the poses of the keyframe maps and correct the position drift inherent in visual odometry. They demonstrate the efficiency of the proposed visual SLAM algorithm for MAV applications in both autonomous and manual flight experiments. The position tracking results are compared to reference data provided by an external tracking system and show promising results. Computer vision allows the localization of a UAV, but it’s dependent on the camera used since feature extraction and tracking algorithms require prior calibration. As noted in [
50], optical flow is sensitive to camera resolution and scene motion rate. The article gives the example of the descent phase of flight, where these parameters change at least a hundred times with altitude.
Bio-inspired alternatives like Rat-SLAM [
28] have attracted attention. They eliminate the need for calibration and have cognition and loop-closing capabilities. Milford et al. describe a biologically inspired approach to SLAM in terrestrial platforms. Rat-SLAM, based on rodent hippocampus models, is coupled to a vision system that provides odometry and appearance information. It builds an online map, driving loop closure and relocalization through sequences of familiar visual scenes. Visual ambiguity is managed by maintaining multiple estimates of vehicle pose, while cumulative errors in odometry are corrected after loop closure by a map correction algorithm. Rat-SLAM demonstrates the system’s mapping performance during a 66 km drive through a complex suburban network. Using a 10 Hz web camera, it generates a real-time map of the environment and closes over 51 loops, up to 5 km in length. NeuroSLAM was inspired by this system [
29]. This 4-DoF proposal uses computational models of three-dimensional grid cells [
27] and multi-layer head direction cells [
26], integrated with a vision system that provides external visual cues and self-motion signals. NeuroSLAM’s neural network generates real-time multi-layer Experience Map (EM), allowing relocalization and loop closure through familiar local visual signals. A multi-layer EM relaxation algorithm corrects errors in path integration after loop closure. Synthetic and real-world datasets show NeuroSLAM generates topologically correct 3D maps.
These last two proposals, although bio-inspired, do not utilize the information processing approach discovered by Neuroscience. For this reason, in this work, we incorporate this form of processing into the central module of Rat-SLAM, modelling each neuron with the MLIF circuit from NC. In this way, once the correct functioning of our proposal is validated, we could potentially implement this module in hardware devices in the future. This would allow us to achieve highly desirable advantages in robotics, such as reducing energy consumption and computational cost, as mentioned in the previous section.
3. Materials and Methods
In this section, we start with an overview of artificial neuron models. Then, in the following two subsections, we will describe the MLIF artificial neuron model and the memristor model.
3.1. Artificial Neuron Model: An Overview
The brains of living beings have been a constant source of inspiration in the development of intelligent systems. Achieving the intrinsic capabilities of the brain, such as its high efficiency in terms of energy consumption as well as information processing, learning, and decision-making, has been highly sought after by scientists [
51,
52,
53,
54,
55]. Researchers have studied and sought ways to model the brain’s components, or neurons, in an attempt to create artificial analogs of the brain. These artificial models would allow the formation of Artificial Neural Networks (ANNs) through their interconnection.
The proposal by McCulloch and Pitts in 1943 [
56] laid the foundation for what is known today as AI. In this first artificial representation of neurons, the information processing is as follows: first, the weighted sum of the neuron inputs is calculated using synaptic weights, and then the result of this mathematical operation is passed through a step activation function. In this way, the state of the neuron is determined by the outcome of this final step. The interconnection of several of these artificial neurons forms a layer. Precisely, the combination of these layers enabled the creation of Multi-Layer Perceptron (MLP) neural networks. The latter has been widely used across different scientific fields [
57,
58,
59,
60,
61]. Later on, other ANN architectures emerged, such as General Regression Neural Networks (GRNN) [
62], Convolutional Neural Networks (CNN) [
63,
64], Long Short Term Memory (LSTM) [
65], Bidirectional Long Short Term Memory (Bi-LSTM) [
66], Graph Convolutional Neural Networks (GCNN) [
67], Extreme Learning Machines (ELM) [
68], to name just a few. However, all these architectures diverge from biological behaviour, as they lack the concept of temporality in input signals. This divergence brings with it the serious disadvantage that processing floating-point numerical signals in ANNs is computationally more expensive compared to the biological processing method based on asynchronous and discrete spike trains [
30]. This is why expensive Graphics Processing Units (GPUs) are generally required in most AI applications.
The search for ANNs whose functioning was more representative of biological behaviour led to different models of artificial neurons, among which the most relevant are the proposals of Hodgkin-Huxley [
69], Izhikevich [
70], and Lapicque [
33,
71]. The latter is better known as Leaky Integrate-and-Fire (LIF). These three ways of artificially modelling neurons are analyzed in [
72], where the following differences between each of these proposals are explained. Hodgkin-Huxley introduced one of the most significant neuronal spiking models from a biophysical standpoint. Designed based on the study of the giant axon of a squid, it was proposed to describe the response of a neuron to external current stimulation and included the effects of different ion channels and leakage currents. The second model was proposed from the study of dynamical systems and bifurcation theory. It involves less than half the equations needed compared to the previous case, and while the model is not biologically realistic, it works well from a phenomenological perspective. Finally, the third model is one of the simplest neuronal spiking models, using only a single differential equation and modelling the neuron’s membrane with a capacitor in parallel with a resistor. Each of these models can be used as building blocks to form the so-called Spiking Neural Networks (SNNs) [
33]. These networks consider the time and nature of neuronal signals, making them a closer model to biological neural networks. SNNs have provided significant insights into information encoding in neural networks, memory, their dynamic behaviour, and, more recently, in deep learning [
73].
An attractive implementation of SNNs is through NC. This offers the opportunity to reduce the massive energy demands of AI applications by implementing computations in brain-inspired computing architectures [
74]. Thus, Lapicque’s proposal can be implemented at the hardware level using the parallel RC electronic circuit. However, certain aspects of this model can be improved by replacing the resistor with a memristor.
As explained in [
75], memristors are a novel technology that goes beyond Complementary Metal Oxide Semiconductors (CMOS). They represent a promising option for memory devices due to their unique intrinsic properties, allowing both storage and processing with a small, massively parallel, and low-power structure. Theoretically, this leads to a significant increase in energy efficiency and computational performance. With this valuable modification, the resulting neuron model, which is a fundamental pillar of our work, is known as MLIF [
35]. In the next subsection, we will explain this model in greater detail.
3.2. Memristive Leaky Integrate-and-Fire Neuron Model
The circuit diagram of the MLIF model used in this work is shown in .
I(
t) is the excitation current crossing the neuronal membrane; C is a capacitor, representing the bilipid membrane;
M is a memristor (whose modelling is explained in the following subsection), analogous to the ionic channel; and
vth is the threshold voltage. When the voltage across the memristor exceeds this threshold, the switch closes, resetting the neuron’s potential to a predefined value, and then reopens until the condition is met again.
. Top: representation of the biological neuron. Bottom: schematic electrical diagram of the MLIF neuron model, where C = 9 × 10<sup>−7</sup> F.
The Equation (1) is the differential equation that models the behaviour of this type of neuron, where
τ =
M(
t)C. To solve this equation, the finite difference method was used, as shown in Equation (2), where ∆
t is the sampling period, with a value of 1 × 10
−3 s adopted in this work.
In this way, the MLIF neuron will generate different spikes in the membrane potential in response to the applied external stimulus, given by the current
I(
t). One case worth analyzing is when the applied external stimulus takes the form of a step function. The neuron responds with an increase in membrane potential until the reset voltage (
vth) is reached, at which point the membrane potential is reset to 0 V, as shown in a. This test allows us to visualize the process of spike generation and how the reset mechanism works when the membrane potential reaches the threshold voltage. Another case worth analyzing is when the neuron is stimulated with a pulse train of varying amplitudes. We observe that during the first excitation condition, the membrane potential increases during the 10 ms that the stimulus is applied and decreases during the following 10 ms when no stimulus is applied, as seen in the first 200 ms of b. Note that in this excitation condition, the duration of each pulse is not sufficient for the membrane potential to reach the threshold voltage, so no reset occurs. Then, there is a pause in the excitation between 200 and 300 ms. After this time interval, we change the amplitude of the excitation current, adopting a non-zero value for 18 ms, and then returning to zero during the next 10 ms. For this condition, the membrane potential increases until it reaches the threshold value, where the potential is reset to zero, as seen in the interval between 300 and 600 ms in b.
. Response of MLIF neuron (<strong>a</strong>) external stimulus is applied by a current step of magnitude equal to 1.5 × 10<sup>−6</sup> A. (<strong>b</strong>) external excitation current stimulus given by a pulse train of varying amplitudes, with a maximum value of 1.5 × 10<sup>−6</sup> A. The reset voltage is equal to 0 V and the threshold voltage <em>V</em><sub>th </sub>is equal to 20 mV.
Electronics is the discipline that has transformed our lives through the development of a vast number of devices. If we inspect these devices at a functional scale, we will see that they are composed of different types of fundamental blocks, which can be classified into active and passive components. Active components include transistors, operational amplifiers, thyristors and others, while passive components are elements that do not contain sources, such as resistors, inductors, and capacitors [
76]. This last group of components continued to be formed by the three mentioned elements until 1971. In that year, Leon Chua proposed the memristor as the fourth passive element in electronics [
34]. Two main characteristics differentiate it from traditional resistors: (1) its ability to vary its resistance value, and (2) having intrinsic memory that allows it to “remember” its last adopted state. These valuable characteristics are a result of its physical composition, shown in . In this diagram, two platinum electrodes are seen, denoted by their chemical symbol (Pt). Between them is a material of length D composed of two layers: one of titanium dioxide (TiO
2), which is highly resistive, and another of oxygen-deficient titanium dioxide (TiO
2−X), which is highly conductive.
. Schematic diagram of the memristor.
The principle of operation is as follows: when an electric current flows in one direction, the boundary
w between the two materials shifts. As a result, the proportion of the TiO
2−X layer increases, causing an increase in the conductivity of the memristor, that is, a decrease in its resistance value. Conversely, when the electric current flows in the opposite direction,
w shifts in the opposite direction compared to the previous case. Therefore, the resistance increases due to a greater proportion of the TiO
2 layer. From this, it follows that when there is no current flow,
w does not change, and the memristor retains its state,
i.e., it “remembers” the last adopted resistance value. Moreover,
w will take different values over time, which is why we will henceforth refer to this parameter as
w(
t).
Mathematically, we model this component using the proposal from HP Labs [
77]. The behaviour of the memristor described in the previous paragraph is given by Equation (3), where
ROFF is the maximum resistance value obtained when
w(
t) = 0, and
RON is the minimum resistance value corresponding to the condition
w(
t)
= D. It is important to note that, at the initial moment
t = 0,
w(
0) will have a value between [0,
D], so the value of the memristor (
M(0)) will lie within the interval [
ROFF,
RON].
The rate of change of
w(
t), considering a linear drift model with average mobility of the oxygen vacancies
μv, is given by Equation (4). Therefore, integrating with respect to time, the value of the location of the boundary between the two regions of the memristor
w(
t) is obtained, as shown in Equation (5). Thus, substituting Equation (5) into Equation (3), we arrive at Equation (6), where $$k = \left(R_{O N} - R_{O F F}\right) \left(\frac{\mu_{v} R_{O N}}{D^{2}}\right)$$.
Solving for the electric charge
q(
t) from Equation (6) and knowing that the limit values the memristor can take are
RON and
ROFF, it is possible to observe the relationship between these two magnitudes, as shown in Equation (7). Then, considering that the variable
k is always less than zero and that the value of the memristor is a monotonically decreasing function of the electric charge, it can be said that the memristor model controlled by the electric charge is a continuous function that is calculated with Equation (8).
On the other hand, it is possible to relate the flux with the electric charge using Equation (9). Solving for the flux from this latter expression, we obtain Equation (10), which, when substituted into Equation (8), allows us to derive the equations governing the behaviour of the flux-controlled memristor model, as shown in Equation (11), where the values of the constants
c3 to
c6 are given by Equation (12).
In this work, the flux-controlled memristor model was used with the parametric values proposed in [
35]. Thus, the values adopted for each of the variables are
ROFF = 20,000 Ω,
RON = 100 Ω,
M(0) = 16,000 Ω, $$\mu_{v} = 1 e^{- 14} \left( \mathrm{m}\right)^{2} \mathrm{s}^{- 1} \mathrm{V}^{- 1}$$, and D = 10 nm. The behaviour of this model is observed in , where the voltage-current hysteresis loop characterizing the memristor for different frequencies of a sinusoidal excitation voltage with an amplitude of 1.5 V is shown.
. Current <i>vs.</i> voltage behaviour in the memristor used.
4. Rat-SLAM for UAV Application
The Rat-SLAM is composed of three main modules: Local View Cell (LVC), Experience Map (EP), and Pose Cell (PC-MLIF). The latter is the most important, and its function is to encode the different poses of the robot in a neural-level representation. The initial applications of this algorithm were in terrestrial environments with three degrees of freedom (position on the plane and orientation) [
28]. However, in underwater or aerial environments, the robot’s degrees of freedom increase from three to six, as it can now move in 3D space and adjust its orientation angles: Roll, Pitch, and Yaw in the Euler representation. This increase in degrees of freedom raises the complexity of the problem since it requires estimating six variables to localize the robot in the environment. However, as UAVs can move independently along all axes, we were able to simplify pose estimation to spatial location (
x,
y,
z) and orientation or Yaw. This allows the use of two PC-MLIF networks: one dedicated to encoding spatial location and another intended to store the orientation corresponding to each position on the plane (
x,
y).
In this work, we adapt the Rat-SLAM algorithm [
28] to operate in aerial environments, as shown in . The first module involved is the environment perception module. Its function is to provide grayscale monocular images, linear velocities, and angular velocity around the
z axis. These come from a monocular camera and an Inertial Measurement Unit (IMU) mounted on the experimental UAV. This environmental information is taken by the second module, the navigation system, where the LVCs receive an image of the environment and the activity centroids of both PC-MLIF networks at each sampling time, establishing a relationship between these three quantities. The LVCs consist of cells that store a visual template for each visited location. When a familiar scene is seen again, the corresponding cell for that view is activated; otherwise, a new cell is created to represent the new view. These visual templates are obtained using the intensity profile of the grayscale image. When the difference between the stored profiles and the current one exceeds a threshold, the current template is stored in a new cell. The comparison between the current profile
Ij and the stored profiles
Ik is performed using the average absolute intensity difference function, as shown in Equation (13). This comparison is performed over a small range of pixel displacements s to provide some robustness against rotation.
. Block diagram and information flow of our Rat-SLAM proposal for aerial environments.
The two PC-MLIF networks are arranged in a prismatic matrix of 3D toroidal grid cells [
27]. Their activity is governed by the dynamics of Continuous Attractor Networks (CAN) [
78]. One of the PC-MLIF networks encodes the location in 3D space, while the other encodes the orientation corresponding to each position in the (
x,
y) plane of the UAV. Each of the component neurons in these networks uses the model explained in Section 3.2, where the excitatory and inhibitory connections are governed by the excitation current entering each neuron, allowing a unique group of units to be active in each possible state. This forms what is called an activity packet or energy packet, whose centroid encodes the current pose estimation of the UAV. The activity in both networks follows the 3D CAN dynamics, which consists of three stages, as explained below. The difference in the update process carried out in each PC-MLIF network lies in the speed used to update the activity along the
z axis. Thus, the PC-MLIF network that encodes the 3D pose uses linear velocity, while the other uses angular velocity. The three update stages are: local excitation, local-global inhibition, and activity normalization. The first stage requires an excitation weight matrix modelled by three-dimensional Gaussian distributions, as shown in Equation (14). In this expression, var represents the variance of each coordinate axis, which is constant for the spatial distribution. The excitation weight matrix, $$\epsilon_{a , b , c}$$, is calculated as the multiplication of the Gaussian distribution for each axis, as seen in Equation (15). The variation in the excitation current is given by Equation (16), where $$n_{x^{'}}$$,$$n_{y^{'}}$$, and $$n_{\theta^{'}}$$ are the dimensions of the activity matrix.
The indices
a,
b, and
c represent the distances between the coordinates
x′,
y′, and
θ′, and are calculated using the expressions shown in Equation (17). The operation
mod(·) returns the remainder of the division of one number by another. It is used to keep the values of the indices
a,
b, and
c within the integers $$\left[0 , \left(n_{x^{'}} - 1\right)\right]$$, $$\left[0 , \left(n_{y^{'}} - 1\right)\right]$$, and $$\left[0 , \left(n_{\theta^{'}} - 1\right)\right]$$, respectively.
Once the variation in excitation current is obtained, the variation in inhibition current is calculated using an inhibitory weight matrix $$\psi_{a , b , c}$$ modelled in the same way as $$\epsilon_{a , b , c }$$, but with negative weight values, as shown in Equation (18).
With these two processes completed, the current applied to each neuron of the PC-MLIF network in the next sampling time is given by Equation (19). As a result of applying a current to each neuron, the membrane potential of each cell is obtained. Each potential represents the activity matrix of the PC-MLIF network, from which a constant value ϕ is subtracted to perform global inhibition, as shown in Equation (20). Finally, it is normalized as shown in Equation (21).
Up to this point, the process of updating activity in the PC-MLIF network has completed the three steps of 3D attractor dynamics, without considering the perceived information from the environment. To incorporate this information into the update process, two steps are performed, known as path integration and local view calibration.The first step projects the activity of the 3D cells to nearby cells by shifting the activity packet in the plane (
x′,
y′) according to linear translational velocity, and in the third dimension according to angular velocity representing the change in heading (
θ′). In Equation (22), the change in the activity matrix due to environmental perception is shown, where $$\delta_{x_{0}^{'}}$$, $$\delta_{y_{0}^{'}}$$ and $$\delta_{\theta_{0}^{'}}$$, are calculated according to Equation (23), with $$k_{x^{'}}$$, $$k_{y^{'}}$$, and $$k_{\theta^{'}}$$ representing the initial offsets for each axis, and $$\gamma$$ is calculated according to Equation (24), where $$\delta_{x_{f}^{'}}$$, $$\delta_{y_{f}^{'}}$$ and $$\delta_{\theta_{f}^{'}}$$are the final offsets given by Equation (25).
The second step is local view calibration. It is aimed at resetting cumulative errors from the trajectory integration. To achieve this, the LVCs are associated with the activity of the two PC-MLIF networks such that when the robot returns to a previously visited location, the LVC associated with this location activates the same neurons in the PC-MLIF network as when this location was first visited, through an excitatory linkage shown with a red dotted arrow in . To learn the relationship between the local view cell vector and the activity in the PC-MLIFs, the matrix ν stores their synaptic interconnections, using a version of Hebb’s law for learning. The connection between $$P_{x^{'} , y^{'} , z^{'} , \theta^{'}}$$ and
Vi is obtained through Equation (26), where
ξ is the learning rate and
Vi is the activity vector of the LVC.
The EM is a topological map composed of many individual experiences,
e, each connected by transitions,
tij. An individual experience
ei, given by Equation (27), contains the positions of the active cells in the PC-MLIF network, $$P_{x^{'} , y^{'} , z^{'} , \theta^{'}}^{i}$$, the activity vector of the LVC (
Vi), and the estimated spatial position (
pi) derived from measurements,
i.e., positions from speed integration. The first experience is created at an arbitrary starting point, and subsequent experiences are built from the previous one through transitions.
When the comparison metric of activity in the two preceding modules exceeds a threshold
Smax, a new experience is created with an associated transition. The metric
S is obtained using Equation (28), where
μp and
μv are constants that weigh the respective contributions of the two PC-MLIF networks and the LVC to the final score.
The transition
tij stores the change in position measured from the integration of velocities obtained from the IMU. Equation (29) shows the stored transitions, where ∆
pij represents the change in the estimated vehicle pose. The link between the previous experience
ei and the new experience
ej is formed according to Equation (30).
Note that a loop closure occurs when the activity in both networks (PC-MLIF and LVC) sufficiently matches a stored experience. When this happens, it is highly unlikely that the accumulated change in position from transitions leads the loop closure experience to match previously stored experiences for the same position. To achieve this match, the positions of all experiences are updated using Equation (31), where α is a constant correction rate,
Nf is the number of links from experience
ei to other experiences, and
Nt is the number of links from other experiences to experience
ei.
5. Experimental Results
5.1. Experimental Setup
To carry out all the experimental tests presented in this section, we will use the well-known Hector Quadrotor simulation environment [
79]. This setup includes a drone equipped with a monocular camera and an IMU to evaluate our proposal. The computational environment is implemented in the Robot Operating System (ROS) [
80], which is widely used in robotics applications due to its many advantages. These include versatility in programming language support, integrated Gazebo and RViz simulators, the ability to simulate different environments and robots, and ease of transition from simulation to real-world deployment.
The Root Mean Squared Error (RMSE) was used as the error metric to assess the accuracy of the trajectory estimates. It is calculated using Equation (32), where
N represents the number of estimates, and,
GT and
EP denote the Ground Truth provided by the drone, published on the /ground_truth/state topic, and Estimated Pose by Rat-SLAM, respectively.
5.2. Performance Evaluation of Rat-SLAM Applied to UAV
For the initial analysis, two trajectories were evaluated. The objective was to determine the suitability of the adapted Rat-SLAM for aerial applications. To this end, the RMSE is calculated for each trajectory relative to the GT, providing a metric to quantify the deviation in Rat-SLAM’s estimates.
The first trajectory is a zig-zag path, shown in . In this path, the drone ascends in a straight line, maintains a constant altitude while moving horizontally, and then descends in a straight line at the endpoint. This trajectory type was selected due to its common use in exploration or inspection tasks.
. Trajectory 1<strong>—</strong>Zig-zag-shaped trajectory. The obtained RMSE was 0.39 m. In (<strong>a</strong>), the trajectory in 3D space is shown, while (<strong>b</strong>) and (<strong>c</strong>) display the projections onto the <em>x</em>-<em>y</em> and <em>x</em>-<em>z</em> planes, respectively.
The corresponding RMSE was 0.39 m. No perturbations were added in this first approach because the main issue we wanted to test is the implementation feasibility of Rat-SLAM with PC-MLIF. A robustness and stability analysis of this approach is still pending, and will be object of further studies.
The second trajectory analyzed evaluates the performance of the proposed approach during a return-to-home path, in which the drone returns to its launch point. This trajectory is common in UAV applications. Unlike the previous test, altitude variations were introduced at different points along this path, providing richer data for analysis. The results, shown in , suggest a slightly higher RMSE compared to the prior evaluation (shown in ), possibly due to the limited number of objects in the environment, which reduces the ability to differentiate between images. This is because the algorithm uses references to landmarks.
. Trajectory 2—with a return to the launch point. The obtained RMSE was 2.95 m. In (<strong>a</strong>), the trajectory in 3D space is shown, while (<strong>b</strong>) and (<strong>c</strong>) display the projections onto the <em>x</em>-<em>y</em> and <em>x</em>-<em>z</em> planes, respectively.
Nonetheless, the observed deviation from the GT falls within the range expected in autonomous robotic systems for wide areas, with an RMSE of 2.95 m. Perhaps a further analysis of cummulative errors and percentual error should be done for applications in a physical drone, as well as a robustness analysis, as mentioned earlier.
5.3. Statistical Analysis of the Memristive 4DoF Rat-Slam
After completing the previous analysis, the second question worth answering is: how is the RMSE influenced if the same trajectory is repeated
n times? Answering this question allows us to determine whether there is a significant deviation in the estimates predicted by Rat-SLAM during successive repetitions. The sequence of steps followed was as follows: (1) the drone is placed at the starting point; (2) the trajectory is executed; (3) once the previous point is reached, the system is reset; and (4) the drone returns to the starting point (1). To obtain a representative sample for performing the statistical analysis, this sequence was repeated
n = 100 times.
To conduct this analysis, we used two trajectories. In the first, the drone travelled from one point to another, covering a considerable distance without returning to the starting point. In the second, it returned to a point near the launch site, covering a smaller area than the first path. and illustrate trajectories 3 and 4, respectively. In these figures, the red trajectory represents the ground truth (GT), the blue dashed line corresponds to the best estimation obtained, and the green dotted line indicates the worst estimation of the algorithm, based on the 100 repetitions performed. These two figures allow us to qualitatively observe the magnitude of the deviation of the best and worst estimates compared to the GT. However, it should be noted that the observed deviations may be because IMU measurements often contain noise, which consequently affects the estimates of our approach during the velocity integration process. We will now analyse the statistical variables calculated for these two trajectories.
. Trajectory 3—the drone moves from one point to another without returning to the launch point. In (<strong>a</strong>), the trajectory is shown in 3D space, while (<strong>b</strong>) and (<strong>c</strong>) show its projections in the <em>x</em>-<em>y </em>and <em>x</em>-<em>z</em> planes, respectively.
. Trajectory 4—the drone follows a path similar to a square, returning to the launch point. In (<strong>a</strong>), the trajectory is shown in 3D space, while (<strong>b</strong>) and (<strong>c</strong>) show its projections in the <em>x</em>-<em>y</em> and <em>x</em>-<em>z</em> planes, respectively.
First, we will focus on the statistical analysis of the localization errors estimated by Rat-SLAM to identify patterns of behaviour under different experimental conditions. We examine both the dispersion and variability of the errors, as well as the properties of the distributions, such as symmetry and kurtosis, to gain a comprehensive understanding of the observed deviations. The results, presented in Table 1 and Table 2, highlight significant differences between the trajectories analysed. On the one hand, trajectory 3 corresponds to a considerable distance travelled without returning to the starting point. This trajectory shows a greater dispersion, with a standard deviation of 0.57m and a range of variation from 3.47 to 6.07 m. This suggests a higher uncertainty in the localization estimated by Rat-SLAM, possibly related to the accumulation of errors in longer or more complex trajectories. In contrast, trajectory 4, which involves a return close to the starting point, shows significantly less variability, with a standard deviation of 0.21 m and a range of variation between 0.74 m and 2.01 m. The lower dispersion in this trajectory suggests greater accuracy in scenarios where the system has the opportunity to close the loop and correct accumulated errors.
.
Descriptive analysis of the two evaluation trajectories.
| Parameter |
Trajectory 3 |
Trajectory 4 |
| Min. [m] |
3.47 |
0.74 |
| Max. [m] |
6.07 |
2.01 |
| Mean [m] |
4.61 |
1.03 |
| Median [m] |
4.58 |
0.96 |
| Standard Deviation [m] |
0.57 |
0.21 |
| Variance [m2] |
4.58 |
0.96 |
| Interquartile Range [m] |
0.83 |
0.11 |
| Kurtosis |
−0.39 |
5.51 |
| Skewness |
0.47 |
2.14 |
.
Hypothesis test.
| Parameter |
Trajectory 3 |
Trajectory 4 |
| Shapiro-Wilk Test |
p-value: 0.02 |
p-value: 0.0001 |
| Runs Test |
p-value: 0.07 |
p-value: 0.0001 |
| Mean Test |
p-value: 0.0001 |
p-value: 0.0001 |
If we analyze the shape measures, for Trajectory 3, the skewness coefficient is 0.47, indicating a slight positive skew. Although most of the errors are concentrated around the mean, the presence of higher values extends the right tail of the distribution, suggesting the occurrence of significantly larger outlier errors, possibly associated with specific segments of the trajectory. This behaviour is confirmed in , where the box plot of the observed errors shows the distribution and dispersion of values, supporting the patterns mentioned for Trajectory 3. The kurtosis of −0.39 indicates a platykurtic distribution, meaning it has less pronounced tails than a normal distribution, suggesting a lower frequency of extreme values and greater dispersion around the mean. Furthermore, the Shapiro-Wilk test confirms the non-normality of the distribution (
p-value = 0.02), while the runs test (
p-value = 0.07) suggests an error pattern close to randomness. These results reinforce the idea that, although variability is moderate, the behaviour of the errors does not follow a fully predictable pattern.
. Box plot of the RMSE of trajectory 3.
In the case of Trajectory 4, the skewness coefficient of 2.14 reveals a marked positive skew. Although most of the errors are relatively small, outliers are identified that represent significantly larger deviations. The kurtosis of 5.51, characteristic of a leptokurtic distribution, indicates a high concentration of errors around the mean, but with long tails that reflect a greater probability of extreme errors, possibly associated with sporadic algorithm failures or external influences. The Shapiro-Wilk test rejects the normality hypothesis (
p-value = 0.0001), confirming the presence of this strong skewness, while the runs test (
p-value = 0.0001) indicates a non-random pattern in the error distribution, suggesting systematic behaviour. In , the box plot corresponding to the errors of this trajectory clearly illustrates this dispersion and the presence of outliers, thus supporting the patterns observed in the statistical measures.
. Box plot of the RMSE of trajectory 4. The mean is shown as an orange dotted line, the frequency distribution is shown in blue, and the black circles represent the outliers obtained in the experimental tests.
The differences in shape measures between both trajectories highlight contrasting dynamics in terms of dispersion and the presence of extreme errors. While Trajectory 1 exhibits a more uniform distribution with a tendency for larger errors, Trajectory 4 is characterized by a more pronounced skew, with a higher concentration of errors near the mean and significant outliers. These results provide a clear insight into the performance of Rat-SLAM under different flight conditions and emphasize the importance of improving its robustness against variations in the perceived environment for each of the evaluated trajectories.
Finally, the hypothesis tests for the mean, with significant p-values in both trajectories (0.0001), confirm that the observed errors deviate from the expected values. However, the magnitude of the errors obtained is within the range of practical values. It is therefore possible to locate a UAV with sufficient accuracy using bio-inspired algorithms, whose information processing is very similar to that of living organisms.
5.4. Comparison of Results: Rat-SLAM vs. EKF
Having answered the previous two questions, the last one worth analyzing is: how much larger or smaller are the estimation errors of Rat-SLAM compared to other types of solutions? In this case, we implemented an EKF, which is a widely used method for the estimation of robot localization through the fusion of GPS and IMU measurements.
The first comparison we made involves a spiral ascent to a height of over thirty meters, as seen in . The goal of this test is to evaluate the behaviour when the position in 3D space is modified simultaneously.
. Trajectory 5<strong>—</strong>spiral ascent: the drone ascends while simultaneously modifying its position in the <em>x</em>-<em>y</em> plane. In (<strong>a</strong>), the GT and the estimates made by the EKF and Rat-SLAM are shown in 3D space, while (<strong>b</strong>) and (<strong>c</strong>) show the projections in the <em>x</em>-<em>y</em> and <em>x</em>-<em>z</em> planes, respectively.
The second comparison is a trajectory where the drone ascends in a straight line, makes a trip, and then returns to the launch point (return to home) without closing the loop, as shown in .
. Trajectory 6—return-to-home trajectory: the drone ascends and then modifies its position in the <em>x</em>-<em>y</em> plane. In (<strong>a</strong>), the GT and the estimates made by the EKF and Rat-SLAM are shown in 3D space, while (<strong>b</strong>) and (<strong>c</strong>) show the projections in the <em>x</em>-<em>y</em> and <em>x</em>-<em>z</em> planes, respectively.
shows the RMSE values, computed according Equation (32), for these trials. By analyzing the magnitude of the errors from both UAV localization solutions, we can conclude that the errors obtained from the present bioinspired approach, are comparable to those obtained by the “classical” EKF. Therefore, it is possible to apply the Rat-SLAM presented in this work to localize a UAV with a bounded error and an appropriate magnitude for such localization applications.
.
Comparison metric between Rat-SLAM and EKF.
| Comparison Trajectory |
RMSE Rat-SLAM [m] |
RMSE EKF [m] |
| Spiral ascent |
0.65 |
0.77 |
| Return-to-home trajectory |
1.49 |
0.68 |
6. Discussion of the Experimental Result
As mentioned in each of the case studies, the goal was to answer different questions that would allow us, on the one hand, to conclude the performance of our memristive based version of Rat-SLAM with Spiking Neural Networks, when used in aerial applications, and on the other hand, to outline a horizon of improvements to be implemented in future work. Additionally, it is important to note that in all the evaluations conducted, the environment we used was highly repetitive. The central idea behind this choice was to analyze whether there is a deep influence on the environment that would make it impossible to use the Rat-SLAM vision system. The repetitiveness of the environment is often a critical factor to consider in vision-based SLAM systems, as in most applications, they cannot be used, requiring the use of additional sensors and/or other algorithms.
The initial evaluations of the system, presented in Section 5.2, aimed to determine the ability of our proposal to solve the SLAM problem in UAV applications. To achieve this, we first evaluated a zig-zag-like trajectory where we observed a much more accurate fit in the x-y plane compared to the x-z plane. The distance travelled by the drone in this initial trajectory was of moderate length. Therefore, the next step was to evaluate a trajectory with a greater distance. The goal was to analyze the quality of the estimates made by Rat-SLAM for long distances. For this, we conducted a trajectory where the drone returns to the launch point, i.e., performs a “return to home”. To do this, we modified the UAV’s pose linearly along the three axes and angularly along the z-axis to allow course adjustment. In this case, there was a higher estimation error in the x-y plane compared to the previous evaluation, while in the x-z plane, the magnitude of the error did not change significantly. These two evaluations allowed us to conclude, both quantitatively and qualitatively, from the RMSE and the pose graphs, respectively, that our proposal is suitable for UAV applications.
The previous conclusion motivated us to continue exploring the behaviour of our algorithm in other operational scenarios. As such, in Section 5.3, we asked how the performance would be if the same trajectory were repeated 100 times. This analysis allows us to determine the influence of the initialization of different variables each time the algorithm is activated. In the first trajectory conducted, the drone moves from one place to another, without returning to the launch point. In this case, we observed that both, the best and worst estimates, were considerably far from the GT. If we compare this trajectory with the one shown in , the one of the returning to launch point, and with a comparable travelled distance, we can appreciate the extreme importance of loop closure to reset the positioning cummulative errors. The deviation observed in the third trajectory (analyzed in Section 5.3) is highly probably caused by the lack of loop closure. In contrast, when the loop closure occurs, the EM restarts the velocity integration errors, adjusting each experience based on this error. The importance of loop closure is evident in trajectory 4 in Section 5.3, where the robot returns to the starting point. In this case, both the worst and best estimates were not as far from the GT. Therefore, one of the future tasks we will undertake is to incorporate a method to reduce the error in velocity integration for cases where the UAV’s trajectory does not return to the starting point.
Finally, we decided to compare the quality of the Rat-SLAM estimates with another method for solving the same positioning problem. To do this, we used an EKF that, by fusing data from the GPS and IMU, estimates the robot’s pose. For these evaluations, we chose to compare the worst-case scenario, that is, the case where the UAV does not perform loop closure. Therefore, if the error of the estimates is within the same order of magnitude as the one obtained by the EKF for the worst-case scenario, we can conclude that our proposal is better for solving SLAM. The first trajectory we performed for this test was a spiral ascent, the Trajectory 5. This allows us to visualize the behaviour when velocities are applied to all three axes simultaneously. If we look at , we can see that the deviations for both the EKF and Rat-SLAM were similar, which is evidenced both graphically and by the RMSE computation. On the other hand, Trajectory 6 involves a return to the starting point, but without closing the loop. For the loop closure to occur, the robot must perceive a known scene, meaning it must pass through the same location again. As expected, in this case, the Rat-SLAM estimates accumulated more error compared to the EKF, primarily in the x-z plane, due to the reasons explained in the previous paragraph. Nevertheless, despite this, we can appreciate that the obtained error magnitude by Rat-SLAM is comparable to that of the EKF approach. Therefore, this allows us to validate the previous hypothesis, in which we questioned the ability of our proposal to solve SLAM with PC-MLIF.
In summary, all the evaluations performed highlighted the need for loop closure, or, if this is not possible, to incorporate some method of reducing integration errors when dealing with trajectories where the robot moves from one point to another. However, it is important to emphasize that the environment is highly repetitive, making it difficult to establish differences between one image and another. Despite this, the algorithm was able to create distinct experiences that allowed it to estimate each of the robot’s poses along the trajectories performed during experimental tests.
7. Conclusions
In this work, we presented a bio-inspired approach to solve SLAM using visual information from the UAV’s environment (from a monocular camera) and inertial information (from an IMU). The use of the MLIF neural model allowed us to further approximate the way information is processed in the brains of living organisms. Moreover, employing this model will enable us, in the future, to utilize memristors for NC based on PC-MLIF networks on a hardware device. This valuable possibility will allow us, on the one hand, to decrease energy consumption by leveraging memristors, and on the other hand, to reduce information processing via software. These characteristics are crucial in autonomous robotic applications, as UAVs have limited onboard software resource capabilities and limited energy availability.
Our version of the well-known Rat-SLAM algorithm is efficient enough to estimate the pose of a robot moving through the air, as well as to construct a semi-metric map of the covered environment using the EM. The magnitude of the errors obtained both when the robot traverses a trajectory once and when it repeats it 100 times, as well as its comparison with the errors from the EKF, demonstrate this estimation efficiency and the ability to solve UAV SLAM with an acceptable error for robotic applications.
In the tests we conducted, we found a limitation in the algorithm operation without closure loops, i.e., without returning to a previously visited location. This occurs because the poses stored in the PC-MLIF network are inferred from linear and angular velocities. If the UAV does not revisit a location that allows the reset of velocity integration errors, they will be accumulated. Therefore, as future work, we propose to include a module to reduce error accumulation during operations without location revisited. This would help mitigate the errors observed in experimental tests where the UAV moves from one point to another without closing the loop. On the other hand, when the loop is closed, that is, when the UAV revisits a previously traversed location, the estimation errors are reset, significantly improving future estimates. This feature makes the algorithm valuable for applications such as package delivery along trajectories that return to the starting point.
Acknowledgments
Author Bernardo Manuel Pirozzo is working towards his PhD with a grant from the National Science and Technological Research Council—CONICET, Argentina. Part of the experimental equipment was acquired through the project PICT 2016 3814‐RIOMAR, from the National Agency of Science and Techological Research, Argentina.
Author Contributions
B.M.P.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing—original draft. G.Y.R.: formal analysis, visualization, writing—review and editing. C.R.R.: investigation, writing—review and editing. S.A.V.: conceptualization, formal analysis, validation, visualization, writing—review and editing. M.D.P.: conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, software, supervision, validation, visualization, writing—review and editing. G.G.A.: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, visualization, writing—review and editing.
Ethics Statement
Not applicable. This studie not involving humans or animals.
Informed Consent Statement
Not applicable. This study does not involve humans in experimentations.
Data Availability Statement
Not informed.
Funding
This research was funded by the National Agency for Scientific and Technological Research (grant PICT 2016 3814—RIOMAR), Argentina, the National University of Buenos Aires Province Center (UNCPBA), Argentina and the National Scientific and Technological Research Council (CONICET), Argentina.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1.
Zalavadiya UB. Drones in agriculture: Mapping, monitoring, and decision-making. In Smart Agritech: Robotics, AI, and Internet of Things (IoT) in Agriculture; Wiley: Hoboken, NJ, USA, 2024; Chapter 14, p. 373.
2.
Singh N, Gupta D, Joshi M, Yadav K, Nayak S, Kumar M, et al. Application of drones technology in agriculture: A modern approach.
J. Sci. Res. Rep. 2024,
30, 142–152.
[Google Scholar]
3.
Restas A. Drone applications for supporting disaster management.
World J. Eng. Technol. 2015,
3, 316–321.
[Google Scholar]
4.
Daud SMSM, Yusof MYPM, Heo CC, Khoo LS, Singh MKC, Mahmood MS, et al. Applications of drone in disaster management: A scoping review.
Sci. Justice 2022,
62, 30–42.
[Google Scholar]
5.
Tuna F. Increasing drones’ combat effectiveness: An alternative analysis for integration into comprehensive military and technological systems.
Uludağ Üniversitesi Fen-Edebiyat Fakültesi Sosyal Bilimler Dergisi 2024,
25, 187–204.
[Google Scholar]
6.
Kim GS, Lee S, Woo T, Park S. Cooperative reinforcement learning for military drones over large-scale battlefields. IEEE Trans. Intell. Veh. 2024, 1–11. doi:10.1109/TIV.2024.3472213.
7.
Wang X, Yang Y, Chan APC, Chi H-L, Yung EHK. A regulatory framework for the use of small unmanned aircrafts (SUAs) in the construction industry.
Eng. Constr. Archit. Manag. 2024,
31, 3024–3049.
[Google Scholar]
8.
Yin Y, Qing L, Wang D, Cheng TCE, Ignatius J. Exact solution method for vehicle-and-drone cooperative delivery routing of blood products.
Comput. Oper. Res. 2024,
164, 106559.
[Google Scholar]
9.
Nguyen NL, Bingi K, Ibrahim R, Korah R, Kumar G, Prusty BR. Autonomous inspection of solar panels and wind turbines using YOLOv8 with quadrotor drones. In Proceedings of the 2024 9th International Conference on Mechatronics Engineering (ICOM), Kuala Lumpur, Malaysia, 13–14 August 2024; pp. 322–326.
10.
Zhang H. Offshore oilfield inspection planning with drone routing optimization.
IEEE Access 2024,
12, 20885–20893.
[Google Scholar]
11.
Macoir N, Bauwens J, Jooris B, Herbruggen BV, Rossey J, Hoebeke J, et al. UWB localization with battery-powered wireless backbone for drone-based inventory management.
Sensors 2019,
19, 467.
[Google Scholar]
12.
Ribeiro MI. Kalman and extended Kalman filters: Concept, derivation and properties.
Inst. Syst. Robot. 2004,
43, 3736–3741.
[Google Scholar]
13.
Kwok C, Fox D, Meila M. Real-time particle filters.
Adv. Neural Inf. Process. Syst. 2002,
15, Available online: https://proceedings.neurips.cc/paper_files/paper/2002/file/2d2ca7eedf739ef4c3800713ec482e1a-Paper.pdf (accessed on 10 March 2024).
[Google Scholar]
14.
Wang W, Li D, Yu W. Simultaneous localization and mapping embedded with particle filter algorithm. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–4.
15.
Ebrahimi M, Mohammadi RK, Sharafi F. The particle filter and extended Kalman filter methods for the structural system identification considering various uncertainties.
Numer. Methods Civ. Eng. 2020,
4, 42–58.
[Google Scholar]
16.
Gageik N, Strohmeier M, Montenegro S. An autonomous UAV with an optical flow sensor for positioning and navigation.
Int. J. Adv. Robot. Syst. 2013,
10, 341.
[Google Scholar]
17.
Yang S, Scherer SA, Yi X, Zell A. Multi-camera visual SLAM for autonomous navigation of micro aerial vehicles.
Robot. Auton. Syst. 2017,
93, 116–134.
[Google Scholar]
18.
Bazargani H, Laganière R. Camera calibration and pose estimation from planes.
IEEE Instrum. Meas. Mag. 2015,
18, 20–27.
[Google Scholar]
19.
Sim R, Dudek G. Learning environmental features for pose estimation.
Image Vis. Comput. 2001,
19, 733–739.
[Google Scholar]
20.
Shan D, Su J, Wang X, Liu Y, Zhou T, Wu Z. VID-SLAM: Robust pose estimation with RGBD-inertial input for indoor robotic localization.
Electronics 2024,
13, 318.
[Google Scholar]
21.
Arafat MY, Moh S. Bio-inspired approaches for energy-efficient localization and clustering in UAV networks for monitoring wildfires in remote areas.
IEEE Access 2021,
9, 18649–18669.
[Google Scholar]
22.
Czy S, Szuniewicz K, Kowalczyk K, Dumalski A, Ogrodniczak M, Zieleniewicz Ł. Assessment of accuracy in unmanned aerial vehicle (UAV) pose estimation with the real-time kinematic (RTK) method on the example of DJI Matrice 300 RTK.
Sensors 2023,
23, 2092.
[Google Scholar]
23.
Ekaso D, Nex F, Kerle N. Accuracy assessment of real-time kinematics (RTK) measurements on unmanned aerial vehicles (UAV) for direct geo-referencing.
Geo-Spat. Inf. Sci. 2020,
23, 165–181.
[Google Scholar]
24.
Huang G, Du S, Wang D. GNSS techniques for real-time monitoring of landslides: A review.
Satell. Navig. 2023,
4, 5.
[Google Scholar]
25.
Fyhn M, Molden S, Witter MP, Moser EI, Moser M-B. Spatial representation in the entorhinal cortex.
Science 2004,
305, 1258–1264.
[Google Scholar]
26.
O’Keefe J, Conway DH. Hippocampal place units in the freely moving rat: Why they fire where they fire.
Exp. Brain Res. 1978,
31, 573–590.
[Google Scholar]
27.
Rank JB. Head-direction cells in the deep layers of dorsal presubiculum of freely moving rats.
Soc. Neurosci. Abstr. 1984,
10, 599.
[Google Scholar]
28.
Milford MJ, Wyeth GF. Mapping a suburb with a single camera using a biologically inspired SLAM system.
IEEE Trans. Robot. 2008,
24, 1038–1053.
[Google Scholar]
29.
Yu F, Shang J, Hu Y, Milford M. NeuroSLAM: A brain-inspired SLAM system for 3D environments.
Biol. Cybern. 2019,
113, 515–545.
[Google Scholar]
30.
Paredes-Vallés F, Scheper KYW, De Croon GCHE. Unsupervised learning of a hierarchical spiking neural network for optical flow estimation: From events to global motion perception.
IEEE Trans. Pattern Anal. Mach. Intell. 2019,
42, 2051–2064.
[Google Scholar]
31.
Vreeken J. Spiking Neural Networks, an Introduction; Utrecht University: Information and Computing Sciences: Utrecht, The Netherlands, 2003.
32.
Marković D, Mizrahi A, Querlioz D, Grollier J. Physics for neuromorphic computing.
Nat. Rev. Phys. 2020,
2, 499–510.
[Google Scholar]
33.
Gerstner W, Kistler WM. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002.
34.
Chua L. Memristor
—The missing circuit element.
IEEE Trans. Circuit Theory 1971,
18, 507–519.
[Google Scholar]
35.
Fang X, Liu D, Duan S, Wang L. Memristive LIF spiking neuron model and its application in Morse code.
Front. Neurosci. 2022,
16, 853010.
[Google Scholar]
36.
Cheng C, Li X, Xie L, Li L. A unmanned aerial vehicle (UAV)/unmanned ground vehicle (UGV) dynamic autonomous docking scheme in GPS-denied environments.
Drones 2023,
7, 613.
[Google Scholar]
37.
Yang B, Yang E, Yu L, Niu C. Adaptive extended Kalman filter-based fusion approach for high-precision UAV positioning in extremely confined environments.
IEEE/ASME Trans. Mechatron. 2022,
28, 543–554.
[Google Scholar]
38.
Li Y, Gao Z, Xu Q, Yang C. Comprehensive evaluations of NLOS and linearization errors on UWB positioning.
Appl. Sci. 2023,
13, 6187.
[Google Scholar]
39.
Mao G, Drake S, Anderson BDO. Design of an extended Kalman filter for UAV localization. In Proceedings of the 2007 Information, Decision and Control, Adelaide, SA, Australia, 12–14 February 2007; pp. 224–229.
40.
Szczepaniak J, Szlachetko B, Lower M. The influence of temporal disturbances in EKF calculations on the achieved parameters of flight control and stabilization of UAVs.
Sensors 2024,
24, 3826.
[Google Scholar]
41.
PX4-ECL GitHub Library. Available online: https://github.com/PX4/PX4-ECL (accessed on 10 March 2024).
42.
Mráz E, Trizuljak A, Rajchl M, Sedláček M, Štec F, Stanko J, et al. Multi-sensor fusion for robust indoor localization of industrial UAVs using particle filter.
J. Electr. Eng. 2024,
75, 304–316.
[Google Scholar]
43.
Chowdhury TJS, Elkin C, Devabhaktuni V, Rawat DB, Oluoch J. Advances on localization techniques for wireless sensor networks: A survey.
Comput. Netw. 2016,
110, 284–305.
[Google Scholar]
44.
Khalaf-Allah M. Particle filtering for three-dimensional TDOA-based positioning using four anchor nodes.
Sensors 2020,
20, 4516.
[Google Scholar]
45.
Rigatos GG. Nonlinear Kalman filters and particle filters for integrated navigation of unmanned aerial vehicles.
Robot. Auton. Syst. 2012,
60, 978–995.
[Google Scholar]
46.
Zhong JP, Fung YF. A biological inspired improvement strategy for particle filters. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, VIC, Australia, 10–13 February 2009; pp. 1–6.
47.
Li M, Li J, Cao Y, Chen G. A dynamic visual SLAM system incorporating object tracking for UAVs.
Drones 2024,
8, 222.
[Google Scholar]
48.
Fischler MA, Bolles RC. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography.
Commun. ACM 1981,
24, 381–395.
[Google Scholar]
49.
Klein G, Murray D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 225–234.
50.
Miller A, Miller B, Popov A, Stepanyan K. UAV landing based on the optical flow videonavigation.
Sensors 2019,
19, 1351.
[Google Scholar]
51.
Chirimuuta M. Your brain is like a computer: Function, analogy, simplification. In Neural Mechanisms: New Challenges in the Philosophy of Neuroscience; Springer: Berlin/Heidelberg, Germany; 2021; pp. 235–261.
52.
Mitchell M. Abstraction and analogy-making in artificial intelligence.
Ann. N. Y. Acad. Sci. 2021,
1505, 79–101.
[Google Scholar]
53.
Konar A. Artificial Intelligence and Soft Computing: Behavioral and Cognitive Modeling of the Human Brain; CRC Press: Boca Raton, FL, USA, 2018.
54.
Burger JR. Human Memory Modeled with Standard Analog and Digital Circuits: Inspiration for Man-Made Computers; John Wiley & Sons: Hoboken, NJ, USA, 2009.
55.
Danchin A, Fenton AA. From analog to digital computing: Is Homo sapiens’ brain on its way to become a Turing machine?
Front. Ecol. Evol. 2022,
10, 796413.
[Google Scholar]
56.
McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity.
Bull. Math. Biophys. 1943,
5, 115–133.
[Google Scholar]
57.
Mfetoum IM, Ngoh SK, Molu RJJ, Kenfack BFN, Onguene R, Naoussi SRD, et al. A multilayer perceptron neural network approach for optimizing solar irradiance forecasting in Central Africa with meteorological insights.
Sci. Rep. 2024,
14, 3572.
[Google Scholar]
58.
Mottaghi H, Masoodi AR, Gandomi AH. Multiscale analysis of carbon nanotube-reinforced curved beams: A finite element approach coupled with multilayer perceptron neural network.
Results Eng. 2024,
23, 102585.
[Google Scholar]
59.
Alghamdi FA, Almanaseer H, Jaradat G, Jaradat A, Alsmadi MK, Jawarneh S, et al. Multilayer perceptron neural network with arithmetic optimization algorithm-based feature selection for cardiovascular disease prediction.
Mach. Learn. Knowl. Extr. 2024,
6, 987–1008.
[Google Scholar]
60.
Palabıyık S, Akkan T. Evaluation of water quality based on artificial intelligence: Performance of multilayer perceptron neural networks and multiple linear regression versus water quality indexes. Environ. Dev. Sustain. 2024, 1–24. doi: 10.1007/s10668-024-05075-6.
61.
Kenas F, Saadia N, Ababou A, Ababou N. Model-free based adaptive finite time control with multilayer perceptron neural network estimation for a 10 DOF lower limb exoskeleton.
Int. J. Adapt. Control Signal Process. 2024,
38, 696–730.
[Google Scholar]
62.
Specht DF. A general regression neural network.
IEEE Trans. Neural Netw. 1991,
2, 568–576.
[Google Scholar]
63.
Zhao X, Wang L, Zhang Y, Han X, Deveci M, Parmar M. A review of convolutional neural networks in computer vision.
Artif. Intell. Rev. 2024,
57, 99.
[Google Scholar]
64.
Chen F, Li S, Han J, Ren F, Yang Z. Review of lightweight deep convolutional neural networks.
Arch. Comput. Methods Eng. 2024,
31, 1915–1937.
[Google Scholar]
65.
Hochreiter S. Long short-term memory. In Neural Computation; MIT Press: Cambridge, MA, USA, 1997.
66.
Schuster M, Paliwal KK. Bidirectional recurrent neural networks.
IEEE Trans. Signal Process. 1997,
45, 2673–2681.
[Google Scholar]
67.
Zhang S, Tong H, Xu J, Maciejewski R. Graph convolutional networks: A comprehensive review.
Comput. Soc. Netw. 2019,
6, 1–23.
[Google Scholar]
68.
Wang J, Lu S, Wang S-H, Zhang Y-D. A review on extreme learning machine.
Multimed. Tools Appl. 2022,
81, 41611–41660.
[Google Scholar]
69.
Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve.
J. Physiol. 1952,
117, 500–544.
[Google Scholar]
70.
Izhikevich EM. Simple model of spiking neurons.
IEEE Trans. Neural Netw. 2003,
14, 1569–1572.
[Google Scholar]
71.
Abbott LF. Lapicque’s introduction of the integrate-and-fire model neuron (1907).
Brain Res. Bull. 1999,
50, 303–304.
[Google Scholar]
72.
Skocik MJ, Long LN. On the capabilities and computational costs of neuron models.
IEEE Trans. Neural Netw. Learn. Syst. 2013,
25, 1474–1483.
[Google Scholar]
73.
Eshraghian JK, Ward M, Neftci EO, Wang X, Lenz G, Dwivedi G, et al. Training spiking neural networks using lessons from deep learning.
Proc. IEEE 2023,
111, 1016–1054.
[Google Scholar]
74.
Krauhausen I, Coen C-T, Spolaor S, Gkoupidenis P, van de Burgt Y. Brain-inspired organic electronics: Merging neuromorphic computing and bioelectronics using conductive polymers.
Adv. Funct. Mater. 2024,
34, 2307729.
[Google Scholar]
75.
Aguirre F, Sebastian A, Le Gallo M, Song W, Wang T, Yang JJ, et al. Hardware implementation of memristor-based artificial neural networks.
Nat. Commun. 2024,
15, 1974.
[Google Scholar]
76.
Isah A, Bilbault J-M. Review on the basic circuit elements and memristor interpretation: Analysis, technology, and applications.
J. Low Power Electron. Appl. 2022,
12, 44.
[Google Scholar]
77.
Strukov DB, Snider GS, Stewart DR, Williams RS. The missing memristor found.
Nature 2008,
453, 80–83.
[Google Scholar]
78.
Samsonovich A, McNaughton BL. Path integration and cognitive mapping in a continuous attractor neural network model.
J. Neurosci. 1997,
17, 5900–5920.
[Google Scholar]
79.
Meyer J, Sendobry A, Kohlbrecher S, Klingauf U, von Stryk O. Comprehensive simulation of quadrotor UAVs using ROS and Gazebo. In Proceedings of the Simulation, Modeling, and Programming for Autonomous Robots: Third International Conference, SIMPAR 2012, Tsukuba, Japan, 5–8 November 2012; Springer: Berlin/Heidelberg, Germany, 2012.
80.
Stanford Artificial Intelligence Laboratory. Robotic Operating System. Available online: https://www.ros.org (accessed on 23 May 2018).